
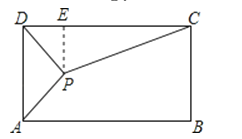
【题目】如图,矩形ABCD中,AB=2AD,AP平分∠DAB,且AP⊥DP于点P,连接CP,则sin∠DCP的值是 .
【答案】![]()
【解析】解:过点P作PE⊥CD于点E,
∵四边形ABCD是矩形,
∴CD=AB,∠DAB=∠ADC=90°.
∵AP是∠DAB的角平分线,
∴∠DAP=![]() ∠DAB=45°.
∠DAB=45°.
∵DP⊥AP,
∴∠APD=90°.
∴∠ADP=45°.
∴∠CDP=45°.
在Rt△APD中,DP=![]() AD,
AD,
在Rt△DEP中,∠DEP=90°,
∴PE=![]() PD=
PD=![]() AD,
AD,
∴CE=CD﹣DE,
∵AB=2AD,
∴CE=CD﹣DE=2AD﹣![]() AD=
AD=![]() AD
AD
在Rt△DEP中,∠CEP=90°,PC=![]() =
=![]() AD,
AD,
∴sin∠DCP=![]() =
=![]() =
=![]() .
.
所以答案是:![]() .
. 
【考点精析】解答此题的关键在于理解矩形的判定方法的相关知识,掌握有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.


科目:初中数学 来源: 题型:
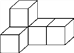
【题目】用5个相同的正方体搭出如图所示的组合体.
(1)分别画出从正面、左面、上面看这个组合体时看到的图形;
(2)如果在这个组合体中,再添加一个相同的正方体组成一个新组合体,从正面、左面看这个新组合体时,看到的图形与原来相同.你认为这个设想能实现吗?若能,画出添加正方体后,从上面看这个组合体时看到的图形;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(米)与时间x(时)的函数图象为线段OA,乙队铺设完的路面长y(米)与时间x(时)的函数图象为折线BC-CD-DE,如图所示,从甲队开始工作时计时.
(1)分别求线段BC、DE所在直线对应的函数关系式.
(2)当甲队清理完路面时,求乙队铺设完的路面长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com