
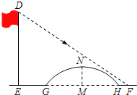
【题目】如图所示,数学小组发现![]() 米高旗杆
米高旗杆![]() 的影子
的影子![]() 落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高
落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高![]() 米,测得其影长为
米,测得其影长为![]() 米,同时测得
米,同时测得![]() 的长为
的长为![]() 米,
米,![]() 的长为
的长为![]() 米,测得小桥拱高(弧
米,测得小桥拱高(弧![]() 的中点到弦
的中点到弦![]() 的距离,即
的距离,即![]() 的长)为
的长)为![]() 米,则小桥所在圆的半径为( )
米,则小桥所在圆的半径为( )
A. ![]() B. 5 C.
B. 5 C. ![]() D. 6
D. 6
【答案】B
【解析】
小桥所在圆的圆心为点O,连结OG,设⊙O的半径为r米.先利用平行投影的性质和相似的性质得到![]() =
=![]() ,于是可求出GH=8米,再根据垂径定理得到点O在直线MN上,GM=HM=
,于是可求出GH=8米,再根据垂径定理得到点O在直线MN上,GM=HM=![]() GH=4米,然后根据勾股定理得到r2=(r2)2+16,再解方程即可.
GH=4米,然后根据勾股定理得到r2=(r2)2+16,再解方程即可.
解答:解:如图,设小桥的圆心为O,连接OM、OG.设小桥所在圆的半径为r米.
∵![]() =
=![]() ,
,
∴![]() =
=![]()
解得EF=12,
∴GH=1231=8(米).
∵MN为弧GH的中点到弦GH的距离,
∴点O在直线MN上,GM=HM=![]() GH=4米.
GH=4米.
在Rt△OGM中,由勾股定理得:OG2=OM2+GM2,
即r2=(r2)2+16,
解得:r=5.
答:小桥所在圆的半径为5米.
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 xOy 中,△ABC 的三个顶点的坐标分别是 A(2,3),B(1,0),C(1,2).
(1)在图中画出△ABC 关于 y 轴对称的![]()
(2)直接写出![]() 三点的坐标:
三点的坐标:
![]() ( ),
( ),![]() ( ),
( ),![]() ( );
( );
(3)如果要使以 B、C、D 为顶点的三角形与△ABC 全等,直接写出所有符合条件的点 D 坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一幅长![]() ,宽
,宽![]() 的风景画的四周外围镶上一条宽度相同的金色纸边,制成一幅挂图,如果要求风景画的面积是整个挂图的
的风景画的四周外围镶上一条宽度相同的金色纸边,制成一幅挂图,如果要求风景画的面积是整个挂图的![]() .若设金色纸边的宽为
.若设金色纸边的宽为![]() .根据题意列方程,并整理得( )
.根据题意列方程,并整理得( )
A. x2-65x+350=0 B. x2+65x-350=0 C. x2+65x-225=0 D. x2-65x+225=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形![]() 中,
中,![]() ,
,![]() ,已知
,已知![]() ,
,![]() ,动点
,动点![]() 从
从![]() 点出发,沿线段
点出发,沿线段![]() 向点
向点![]() 作匀速运动:动点
作匀速运动:动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向点
向点![]() 作匀速运动.过
作匀速运动.过![]() 点垂直于
点垂直于![]() 的射线交
的射线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.![]() 、
、![]() 两点同时出发,速度都为每秒
两点同时出发,速度都为每秒![]() 个单位长度.当
个单位长度.当![]() 点运动到
点运动到![]() 点,
点,![]() 、
、![]() 两点同时停止运动.设点
两点同时停止运动.设点![]() 运动的时问为
运动的时问为![]() 秒.
秒.

![]() ________,
________,![]() ________.(用
________.(用![]() 的代数式表示);
的代数式表示);
![]() 当
当![]() 为何值时,四边形
为何值时,四边形![]() 构成平行四边形?
构成平行四边形?
![]() 若
若![]() 为等腰三角形,求
为等腰三角形,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
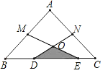
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() 为
为![]() 上的点,连接
上的点,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,
,![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )
A. 1cm2 B. 1.5cm2 C. 2cm2 D. 3cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣bx+c交x轴于点A(1,0),交y轴于点B,对称轴是x=2.

(1)求抛物线的解析式;
(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形![]() 中,
中,![]() ,
,![]() ,两条对角线相交于点
,两条对角线相交于点![]() .以
.以![]() 、
、![]() 为邻边作第
为邻边作第![]() 个平行四边形
个平行四边形![]() ,对角线相交于点
,对角线相交于点![]() ;再以
;再以![]() 、
、![]() 为邻边作第
为邻边作第![]() 个平行四边形
个平行四边形![]() ,对角线相交于点
,对角线相交于点![]() ;再以
;再以![]() 、
、![]() 为邻边作第
为邻边作第![]() 个平行四边形
个平行四边形![]() …依此类推.
…依此类推.

![]() 求矩形
求矩形![]() 的面积;
的面积;
![]() 求第
求第![]() 个平行四边形
个平行四边形![]() ,第
,第![]() 个平行四边形和第
个平行四边形和第![]() 个平行四边形的面积.
个平行四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是________(填A或B或C)
A.a2-2ab+b2=(a-b)2
B.a2-b2=(a+b)(a-b)
C.a2+ab=a(a+b)
(2)应用你从(1)中选出的等式,完成下列各题:
①已知x2-4y2=12,x+2y=4,求x-2y的值
②计算:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )…(1-
)…(1-![]() )(1-
)(1-![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com