
【题目】如图,在平面直角坐标系 xOy 中,△ABC 的三个顶点的坐标分别是 A(2,3),B(1,0),C(1,2).
(1)在图中画出△ABC 关于 y 轴对称的![]()
(2)直接写出![]() 三点的坐标:
三点的坐标:
![]() ( ),
( ),![]() ( ),
( ),![]() ( );
( );
(3)如果要使以 B、C、D 为顶点的三角形与△ABC 全等,直接写出所有符合条件的点 D 坐标.

【答案】(1)见解析;(2)![]() (-2,3),
(-2,3),![]() (-1,0),
(-1,0),![]() (-1,2);(3)(0,3),(0,-1),(2,-1).
(-1,2);(3)(0,3),(0,-1),(2,-1).
【解析】
(1)利用轴对称变换,即可作出△ABC关于y轴对称的△A1B1C1;
(2)由(1)中的直角坐标系可直接得出![]() 三点的坐标;
三点的坐标;
(3)依据以B、C、D为顶点的三角形与△ABC全等,可知两个三角形有公共边BC,运用对称性即可得出所有符合条件的点D坐标.
(1)如图所示,△A1B1C1即为所求;

(2)由(1)中直角坐标系可得
![]() (-2,3),
(-2,3),![]() (-1,0),
(-1,0),![]() (-1,2);
(-1,2);
(3)当△BCD与△BCA关于BC对称时,点D坐标为(0,3),
当△BCA与△CBD关于BC的中点对称时,点D坐标为(0,-1),
△BCA与△CBD关于BC的中垂线对称时,点D坐标为当(2,-1).


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
【题目】在“抛硬币”游戏中,抛![]() 次出现
次出现![]() 次正面;抛
次正面;抛![]() 次出现
次出现![]() 次正面;抛
次正面;抛![]() 次出现
次出现![]() 次正面;抛
次正面;抛![]() 次出现
次出现![]() 次正面.试问:
次正面.试问:
![]() 四次抛硬币,出现正面的频率各是________、________、______、_______.
四次抛硬币,出现正面的频率各是________、________、______、_______.
![]() 用一句话概括出游戏中的规律________.
用一句话概括出游戏中的规律________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点D是BC的中点
,点D是BC的中点![]() 作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
![]() 试猜想线段BG和AE的数量关系是______;
试猜想线段BG和AE的数量关系是______;
![]() 将正方形DEFG绕点D逆时针方向旋转
将正方形DEFG绕点D逆时针方向旋转![]() ,
,
![]() 判断
判断![]() 中的结论是否仍然成立?请利用图2证明你的结论;
中的结论是否仍然成立?请利用图2证明你的结论;
![]() 若
若![]() ,当AE取最大值时,求AF的值.
,当AE取最大值时,求AF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( )

A. 1 B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设![]() ,
,![]() .
.
①如图2,当点在线段BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自定义:在一个图形上画一条直线,若这条直线既平分该图形的面积,又平分该图形的周长,我们称这条直线为这个图形的“等分积周线”.
(1)如图1,已知△ABC,AC≠BC,过点C能否画出△ABC的一条“等分积周线”?若能,说出确定的方法,若不能,请说明理由.
(2)如图2,在四边形ABCD中,∠B=∠C=90°,EF垂直平分AD,垂足为F,交BC于点E,已知AB=3,BC=8,CD=5.求证:直线EF为四边形ABCD的“等分积周线”;
(3)如图3,在△ABC中,AB=BC=6,AC=8,请你画出△ABC的一条“等分积周线”EF(要求:直线EF不过△ABC的顶点,交边AC于点F,交边BC于点E),并说明EF为“等分积周线”的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
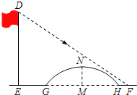
【题目】如图所示,数学小组发现![]() 米高旗杆
米高旗杆![]() 的影子
的影子![]() 落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高
落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高![]() 米,测得其影长为
米,测得其影长为![]() 米,同时测得
米,同时测得![]() 的长为
的长为![]() 米,
米,![]() 的长为
的长为![]() 米,测得小桥拱高(弧
米,测得小桥拱高(弧![]() 的中点到弦
的中点到弦![]() 的距离,即
的距离,即![]() 的长)为
的长)为![]() 米,则小桥所在圆的半径为( )
米,则小桥所在圆的半径为( )
A. ![]() B. 5 C.
B. 5 C. ![]() D. 6
D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com