
【题目】如图,直角梯形![]() 中,
中,![]() ,
,![]() ,已知
,已知![]() ,
,![]() ,动点
,动点![]() 从
从![]() 点出发,沿线段
点出发,沿线段![]() 向点
向点![]() 作匀速运动:动点
作匀速运动:动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向点
向点![]() 作匀速运动.过
作匀速运动.过![]() 点垂直于
点垂直于![]() 的射线交
的射线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.![]() 、
、![]() 两点同时出发,速度都为每秒
两点同时出发,速度都为每秒![]() 个单位长度.当
个单位长度.当![]() 点运动到
点运动到![]() 点,
点,![]() 、
、![]() 两点同时停止运动.设点
两点同时停止运动.设点![]() 运动的时问为
运动的时问为![]() 秒.
秒.

![]() ________,
________,![]() ________.(用
________.(用![]() 的代数式表示);
的代数式表示);
![]() 当
当![]() 为何值时,四边形
为何值时,四边形![]() 构成平行四边形?
构成平行四边形?
![]() 若
若![]() 为等腰三角形,求
为等腰三角形,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;
; ![]()
![]() ;
; ![]() 当
当![]() ,
,![]() ,
,![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
【解析】
(1)由题意易知四边形ABNQ是矩形,从而可得NC=BC-BN=BC-AQ,由AQ=AD-QD=3-t即可求得NC的长,在Rt△ABC中,利用勾股定理求得AC的长,然后在Rt△MNC中,利用cos∠NCM=![]() ,即可求得CM的长;
,即可求得CM的长;
(2)四边形PCDQ构成平行四边形就是PC=DQ,可得方程4-t=t,解方程即可得;
(3)分三种情况分别进行讨论即可得答案.
![]() 由题意易得四边形ABNQ是矩形,
由题意易得四边形ABNQ是矩形,
∴BN=AQ,
∵DQ=t,AQ=AD-DQ,
∴![]() ,
,
∴![]() =BC-BN=4-AQ
=BC-BN=4-AQ![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ;
;
![]() 由于四边形
由于四边形![]() 构成平行四边形,
构成平行四边形,
∴![]() ,即
,即![]() ,
,
解得![]() ;
;
![]() ①当
①当![]() 时(如图),
时(如图),
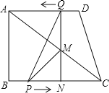
则有:![]() ,
,
即![]() ,
,
∴![]() ,
,
解得:![]() ;
;
②当![]() 时(如图),
时(如图),
则有:![]() ,
,
解得:![]() ;
;
③当![]() 时(如图),
时(如图),
在![]() 中,
中,![]()
而![]() ,
,![]() ,
,
∴![]()
![]() ,
,
解得:![]() ,
,![]() (舍去),
(舍去),
∴当![]() ,
,![]() ,
,![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.


科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P的坐标为(-3,4),作出点P关于x轴对称的点P1,称为第1次变换;再作出点P1关于y轴对称的点P2,称为第2次变换;再作点P2关于x轴对称的点P3,称为第3次变换,…,依次类推,则第2019次变换得到的点P2019的坐标为 ____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽和小华想利用摸球游戏决定谁去参加市里举办的书法比赛,游戏规则是:在一个不透明的袋子里装有除数字外完全相同的4个小球,上面分别标有数字2,3,4,5.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为偶数,则小丽去参赛;否则小华去参赛.
(1)用列表法或画树状图法,求小丽参赛的概率.
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,数学小组发现![]() 米高旗杆
米高旗杆![]() 的影子
的影子![]() 落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高
落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高![]() 米,测得其影长为
米,测得其影长为![]() 米,同时测得
米,同时测得![]() 的长为
的长为![]() 米,
米,![]() 的长为
的长为![]() 米,测得小桥拱高(弧
米,测得小桥拱高(弧![]() 的中点到弦
的中点到弦![]() 的距离,即
的距离,即![]() 的长)为
的长)为![]() 米,则小桥所在圆的半径为( )
米,则小桥所在圆的半径为( )
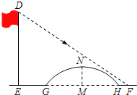
A. ![]() B. 5 C.
B. 5 C. ![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=12cm,BC=6cm,D为BC的中点,动点P从B点出发,以每秒1cm的速度沿B→A→C的方向运动,设运动时间为t,那么当t=_________秒时,过D、P两点的直线将△ABC的周长分成两个部分,使其中一部分是另一部分的2倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究应用:
(1)计算:![]() ;
;![]() .
.
(2)上面的乘法计算结果很简洁,你发现了什么规律(公式)?用含![]() 、
、![]() 的字母表示该公式为: .
的字母表示该公式为: .
(3)下列各式能用第(2)题的公式计算的是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要建一个面积为140平方米的仓库,仓库的一边靠墙,这堵墙长16米;在与墙平行的一边,要开一扇2米宽的门.已知围建仓库的现有木板材料可使新建板墙的总长为32米,那么这个仓库设计的长和宽应分别为多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com