
【题目】如图,点![]() 都在反比例函数
都在反比例函数![]() 的图象上.
的图象上.
(1)求![]() 的值;
的值;
(2)如果![]() 为
为![]() 轴上一点,
轴上一点,![]() 为
为![]() 轴上一点,以点
轴上一点,以点![]() 为顶点的四边形是平行四边形,试求直线
为顶点的四边形是平行四边形,试求直线![]() 的函数表达式;
的函数表达式;
(3)将线段![]() 沿直线
沿直线![]() 进行对折得到线段
进行对折得到线段![]() ,且点
,且点![]() 始终在直线
始终在直线![]() 上,当线段
上,当线段![]() 与
与![]() 轴有交点时,则
轴有交点时,则![]() 的取值范围为_______(直接写出答案)
的取值范围为_______(直接写出答案)
【答案】(1)m=3,k=12;(2)y![]() x+2或y
x+2或y![]() x﹣2;(3)
x﹣2;(3)![]() .
.
【解析】
(1)由题可得m(m+1)=(m+3)(m﹣1)=k,解这个方程就可求出m、k的值.
(2)由于点A、点B是定点,可对线段AB进行分类讨论:AB是平行四边形的边、AB是平行四边形的对角线,再利用平行四边形的性质、中点坐标公式及直线的相关知识就可解决问题.
(3)由于点A关于直线y=kx+b的对称点点A1始终在直线OA上,因此直线y=kx+b必与直线OA垂直,只需考虑两个临界位置(A1在x轴上、B1在x轴上)对应的b的值,就可以求出b的取值范围.
(1)∵点A(m,m+1),B(m+3,m﹣1)都在反比例函数y![]() 的图象上,∴m(m+1)=(m+3)(m﹣1)=k.
的图象上,∴m(m+1)=(m+3)(m﹣1)=k.
解得:m=3,k=12,∴m、k的值分别为3、12.
(2)设点M的坐标为(m,0),点N的坐标为(O,n).
①若AB为平行四边形的一边.
Ⅰ.点M在x轴的正半轴,点N在y轴的正半轴,连接BN、AM交于点E,连接AN、BM,如图1.
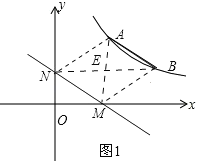
∵四边形ABMN是平行四边形,∴AE=ME,NE=BE.
∵A(3,4)、B(6,2)、M(m,0)、N(0,n),∴由中点坐标公式可得:
xE![]() ,yE
,yE![]() ,∴m=3,n=2,∴M(3,0)、N(0,2).
,∴m=3,n=2,∴M(3,0)、N(0,2).
设直线MN的解析式为y=kx+b.
则有![]()
解得: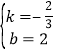 ,∴直线MN的解析式为y
,∴直线MN的解析式为y![]() x+2.
x+2.
Ⅱ.点M在x轴的负半轴,点N在y轴的负半轴,连接BM、AN交于点E,连接AM、BN,如图2,同理可得:直线MN的解析式为y![]() x﹣2.
x﹣2.
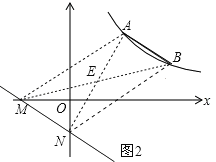
②若AB为平行四边形的一条对角线,连接AN、BM,设AB与MN交于点F,如图3.
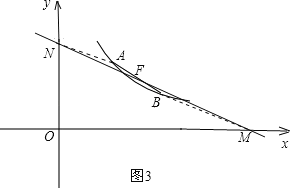
同理可得:直线MN的解析式为y![]() x+6,此时点A、B都在直线MN上,故舍去.
x+6,此时点A、B都在直线MN上,故舍去.
综上所述:直线MN的解析式为y![]() x+2或y
x+2或y![]() x﹣2.
x﹣2.
(3)①当点B1落到x轴上时,如图4.
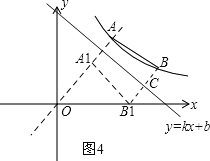
设直线OA的解析式为y=ax.
∵点A的坐标为(3,4),∴3a=4,即a![]() ,∴直线OA的解析式为y
,∴直线OA的解析式为y![]() x.
x.
∵点A1始终在直线OA上,∴直线y=kx+b与直线OA垂直,∴![]() k=﹣1,∴k
k=﹣1,∴k![]() .
.
由于BB1∥OA,因此直线BB1可设为y![]() x+c.
x+c.
∵点B的坐标为(6,2),∴![]() 6+c=2,即c=﹣6,∴直线BB1解析式为y
6+c=2,即c=﹣6,∴直线BB1解析式为y![]() x﹣6.
x﹣6.
当y=0时,![]() x﹣6=0.则有x
x﹣6=0.则有x![]() ,∴点B1的坐标为(
,∴点B1的坐标为(![]() ,0).
,0).
∵点C是BB1的中点,∴点C的坐标为(![]() )即(
)即(![]() ,1).
,1).
∵点C在直线y![]() x+b上,∴
x+b上,∴![]() b=1.
b=1.
解得:b![]() .
.
②当点A1落到x轴上时,如图5.
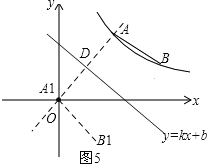
此时,点A1与点O重合.
∵点D是AA1的中点,A(3,4),A1(0,0),∴D(![]() ,2).
,2).
∵点D在直线y![]() x+b上,∴
x+b上,∴![]() b=2.
b=2.
解得:b![]() .
.
综上所述:当线段A1B1与x轴有交点时,则b的取值范围为![]() .
.
故答案为:![]() .
.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
(1)求反比例函数的表达式;
(2)根据图象直接写出﹣![]() x>
x>![]() 的解集;
的解集;
(3)将直线l1:y=- ![]() x沿y向上平移后的直线l2与反比例函数y=
x沿y向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(﹣1,0),B(4,0),C(0,3)三点,D为直线BC上方抛物线上一动点,DE⊥BC于E.

(1)求抛物线的函数表达式;
(2)如图1,求线段DE长度的最大值;
(3)如图2,设AB的中点为F,连接CD,CF,是否存在点D,使得△CDE中有一个角与∠CFO相等?若存在,求点D的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OB,垂足为M,DE=4,连接AD,过E作AD平行线交AB延长线于点C.
(1)求⊙O的半径;
(2)求证:CE是⊙O的切线;
(3)若弦DF与直径AB交于点N,当∠DNB=30°时,求图中阴影部分的面积.
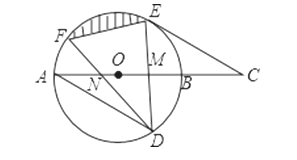
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮组成团队参加某科学比赛.该比赛的规则是:每轮比赛一名选手参加,若第一轮比赛得分满60则另一名选手晋级第二轮,第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩,两人在赛前分别作了九次测试,如图为二人测试成绩折线统计图,下列说法合理的是( )
①小亮测试成绩的平均数比小明的高;②小亮测试成绩比小明的稳定;③小亮测试成绩的中位数比小明的高;④小亮参加第一轮比赛,小明参加第二轮比赛,比较合理.
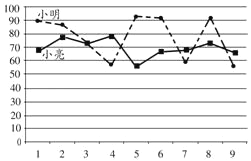
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个正整数m,如果![]() ,其中n是正整数,则称m为“优数”,n为m的最优拆分点,例如:
,其中n是正整数,则称m为“优数”,n为m的最优拆分点,例如:![]() ,则72是一个“优数”,8为72的最优拆分点.
,则72是一个“优数”,8为72的最优拆分点.
![]() 请写出一个大于40小于50的“优数”______,它的最优拆分点是______.
请写出一个大于40小于50的“优数”______,它的最优拆分点是______.
![]() 把“优数”p的2倍与“优数”q的3倍的差记为
把“优数”p的2倍与“优数”q的3倍的差记为![]() ,例如:
,例如:![]() ,
,![]() ,则
,则![]() 若“优数”p的最优拆分点为
若“优数”p的最优拆分点为![]() ,“优数”q的最优拆分点为t,当
,“优数”q的最优拆分点为t,当![]() 时,求t的值并判断它是否为“优数”.
时,求t的值并判断它是否为“优数”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com