
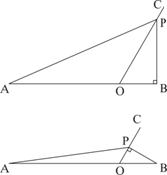
如图(1),线段AB与射线OC相交于点O,且∠BOC=60°,AO=3,OB=1,动点P以每秒1个单位长度的速度从点O出发,在射线OC做匀速运动,设运动时间为t秒.
(1)当t=3秒时,则OP= , = ;
= ;
(2)当△OPB是直角三角形时,求t的值;
(3)如图(2),当AP=AB,过点A作AQ∥BP,并使得∠QOP=∠B,连接QP,QO、AP交于点F,试证明△APQ∽△BPO。

解:(1)OP=3, =3:4 4分
=3:4 4分
 (2)①∵∠BOP=60°∴∠BOP不为直角; 5分
(2)①∵∠BOP=60°∴∠BOP不为直角; 5分
②当∠OBP=90°时,如图所示
∵∠BOP=60°∴∠OPB=30°
∴OP=2OB,
∴t=2s 7分
③当∠OPB=90°时,如图所示
∵∠BOP=60°∴∠OBP=30°
∴OB=2OP,
∴2t=1 ∴t= s 8分
s 8分
综上,当△OPB为直角三角形时,t=2s或 s 9分
s 9分
(3) ∵AQ∥BP,
∴ ∠QAP=∠APB
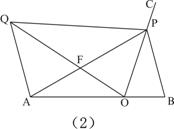 ∵ AP=AB
∵ AP=AB
∴∠APB=∠B ∴ ∠QAP=∠B
又∵ ∠QOP=∠B
∴ ∠QAP=∠QOP
又∵∠QFA=∠PFO
∴ △QFA∽△PFO
∴ 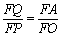 , 11分
, 11分
即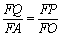 12分
12分
又∵ ∠PFQ=∠OFA,
∴ △PFQ∽△OFA 13分
∴ ∠QPA=∠QOA.
∵ ∠AOC=∠OPB+∠B=∠QOA+∠QOP,∠B=∠QOP,
∴∠QOA=∠OPB ∴∠OPB =∠QPA.
∴ △APQ∽△BPO.


科目:初中数学 来源: 题型:
已知一元二次方程x2﹣4x+k=0有两个实数根.
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
在舞台上有两根竖直放置的铁杆,其中铁杆AB长1m,CD长2m,两根铁杆之间的距离为3m,现在B、D之间拉起一根钢索,杂技演员在上面表演走钢丝,为了描述演员的位置,小明以A点为坐标原点,建立了如图所示的平面直角坐标系,演员的位置为点M,设其横坐标为x,纵坐标为y。
(1)写出线段BD的函数关系式;
(2)为了保护演员的安全,过D点拉了一根与地面平行的钢索DE,在上面挂上了一条保险钢丝MN,MN随演员的移动而移动,并始终垂直于地面,其长度自动调整,设保险钢丝的长度为w,求w与x之间的函数关系式。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com