
ЁОЬтФПЁПФГЪаНЋОйАьЁАЪБДњаТШЫЫЕЁБЕкШ§МОЃЌавИЃдАаЁЧјОгЮЏЛсЮЊСЫНтОгУёЛёШЁЁАЪБДњаТШЫЫЕЁБЛюЖЏЯрЙиаХЯЂЕФЗНЪННјааСЫЫцЛњГщбљЕїВщЃЌЕїВщЩшжУСЫA(ЭјТч)ЃЌB(ЕчЪг)ЃЌC(БЈжН)ЃЌD(ЦфЫћ)ЫФжжЗНЪНЃЌБЛЕїВщЕФОгУёжЛФмДгжабЁШЁвЛжжЗНЪНЃЌВЂИљОнЪеМЏЕНЕФЪ§ОнЛцжЦСЫШчЯТЕФСНЗљОљВЛЭъећЕФЭГМЦЭМЃК
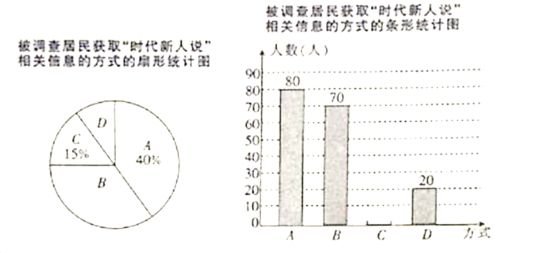
ИљОнЭМжааХЯЂЃЌНтД№ЯТСаЮЪЬтЃЎ
![]() ВЙШЋЩЯУцЕФЬѕаЮЭГМЦЭМЃЎ
ВЙШЋЩЯУцЕФЬѕаЮЭГМЦЭМЃЎ
![]() дкЩШаЮЭГМЦЭМжаЃЌбЁдё
дкЩШаЮЭГМЦЭМжаЃЌбЁдё![]() жжЗНЪНЕФШЫЪ§ЫљеМЕФАйЗжБШЪЧ ЃЌбЁдё
жжЗНЪНЕФШЫЪ§ЫљеМЕФАйЗжБШЪЧ ЃЌбЁдё![]() жжЗНЪНЕФШЫЪ§ЫљдкЩШаЮдВаФНЧЕФЖШЪ§ЪЧ ЃЎ
жжЗНЪНЕФШЫЪ§ЫљдкЩШаЮдВаФНЧЕФЖШЪ§ЪЧ ЃЎ
![]() ИУаЁЧјга
ИУаЁЧјга![]() Фа
Фа![]() ХЎБЈУћСЫЩчЧјЕФЁАЪБДњаТШЫЫЕЁБЛюЖЏЃЌгЩгкШЫЪ§ЯожЦЃЌОгЮЏЛсжЛФмДгжаЫцЛњГщШЁ
ХЎБЈУћСЫЩчЧјЕФЁАЪБДњаТШЫЫЕЁБЛюЖЏЃЌгЩгкШЫЪ§ЯожЦЃЌОгЮЏЛсжЛФмДгжаЫцЛњГщШЁ![]() УћВЮМгЛюЖЏЃЌЧыФугУЛЪїзДЭМЛђСаБэЕФЗНЗЈЧѓГіЧЁКУГщЕН
УћВЮМгЛюЖЏЃЌЧыФугУЛЪїзДЭМЛђСаБэЕФЗНЗЈЧѓГіЧЁКУГщЕН![]() Фа
Фа![]() ХЎЕФИХТЪЃЎ
ХЎЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЭЈЙ§ЙлВьЩШаЮЭГМЦЭМКЭЬѕаЮЭГМЦЭМЃЌЕУЕНбЁдё![]() жжЗНЪНЕФШЫЪ§КЭЫљеМЕФАйЗжБШЃЌгУбЁдё
жжЗНЪНЕФШЫЪ§КЭЫљеМЕФАйЗжБШЃЌгУбЁдё![]() жжЗНЪНЕФШЫЪ§Г§вдбЁдё
жжЗНЪНЕФШЫЪ§Г§вдбЁдё![]() жжЗНЪНЕФШЫЪ§ЫљеМЕФАйЗжБШЃЌМДПЩЕУЕНВЮМгЕїВщЕФзмШЫЪ§ЃЌгУзмШЫЪ§ГЫвдбЁдё
жжЗНЪНЕФШЫЪ§ЫљеМЕФАйЗжБШЃЌМДПЩЕУЕНВЮМгЕїВщЕФзмШЫЪ§ЃЌгУзмШЫЪ§ГЫвдбЁдё![]() жжЗНЪНЕФШЫЪ§ЫљеМЕФАйЗжБШЃЌМДПЩЕУЕНбЁдё
жжЗНЪНЕФШЫЪ§ЫљеМЕФАйЗжБШЃЌМДПЩЕУЕНбЁдё![]() жжЗНЪНЕФШЫЪ§ЃЌОнДЫМДПЩВЙШЋЬѕаЮЭГМЦЭМЃЎ
жжЗНЪНЕФШЫЪ§ЃЌОнДЫМДПЩВЙШЋЬѕаЮЭГМЦЭМЃЎ
ЃЈ2ЃЉгУбЁдё![]() жжЗНЪНЕФШЫЪ§Г§вдВЮМгЕїВщЕФзмШЫЪ§ЃЌМДПЩЕУЕНбЁдё
жжЗНЪНЕФШЫЪ§Г§вдВЮМгЕїВщЕФзмШЫЪ§ЃЌМДПЩЕУЕНбЁдё![]() жжЗНЪНЕФШЫЪ§ЫљеМЕФАйЗжБШЃЛгУ
жжЗНЪНЕФШЫЪ§ЫљеМЕФАйЗжБШЃЛгУ![]() ГЫвдбЁдё
ГЫвдбЁдё![]() жжЗНЪНЕФШЫЪ§ЫљеМЕФАйЗжБШЃЌМДПЩЕУЕНбЁдё
жжЗНЪНЕФШЫЪ§ЫљеМЕФАйЗжБШЃЌМДПЩЕУЕНбЁдё![]() жжЗНЪНЕФШЫЪ§ЫљдкЩШаЮдВаФНЧЕФЖШЪ§ЃЎ
жжЗНЪНЕФШЫЪ§ЫљдкЩШаЮдВаФНЧЕФЖШЪ§ЃЎ
ЃЈ3ЃЉИљОнЬтвтСаГіБэИёЃЌЫуГіЫљгаЕШПЩФмЕФНсЙћЪ§КЭЧЁКУГщЕН![]() Фа
Фа![]() ХЎЕФНсЙћЪ§ЃЌгУЧЁКУГщЕН
ХЎЕФНсЙћЪ§ЃЌгУЧЁКУГщЕН![]() Фа
Фа![]() ХЎЕФНсЙћЪ§Г§вдЫљгаЕШПЩФмЕФНсЙћЪ§ЃЌМДЕУЕНЧЁКУГщЕН
ХЎЕФНсЙћЪ§Г§вдЫљгаЕШПЩФмЕФНсЙћЪ§ЃЌМДЕУЕНЧЁКУГщЕН![]() Фа
Фа![]() ХЎЕФИХТЪЃЎ
ХЎЕФИХТЪЃЎ
НтЃКЃЈ1ЃЉЁп![]() ЃЌ
ЃЌ
ЁрВЮМгЕїВщЕФзмШЫЪ§ЪЧ200ШЫЃЌ
ЁрбЁдё![]() жжЗНЪНЕФШЫЪ§ЮЊЃК
жжЗНЪНЕФШЫЪ§ЮЊЃК![]() ЃЈШЫЃЉЃЌ
ЃЈШЫЃЉЃЌ
дђВЙШЋЬѕаЮЭГМЦЭМШчЯТЃК
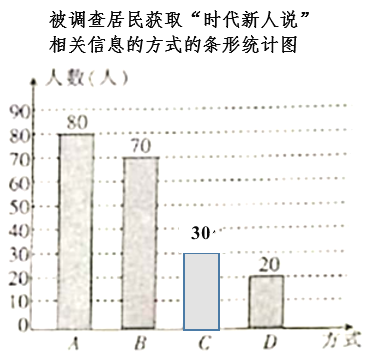
ЃЈ2ЃЉЁп![]() ЃЌ
ЃЌ
ЁрВЮМгЕїВщЕФзмШЫЪ§ЪЧ200ШЫЃЌ
ЁрбЁдё![]() жжЗНЪНЕФШЫЪ§ЫљеМЕФАйЗжБШЮЊЃК
жжЗНЪНЕФШЫЪ§ЫљеМЕФАйЗжБШЮЊЃК![]() ЃЌ
ЃЌ
МДбЁдё![]() жжЗНЪНЕФШЫЪ§ЫљеМЕФАйЗжБШЪЧ
жжЗНЪНЕФШЫЪ§ЫљеМЕФАйЗжБШЪЧ![]() ЃЌ
ЃЌ
ЁпбЁдё![]() жжЗНЪНЕФШЫЪ§ЫљеМЕФАйЗжБШЪЧ
жжЗНЪНЕФШЫЪ§ЫљеМЕФАйЗжБШЪЧ![]() ЃЌ
ЃЌ
ЁрбЁдё![]() жжЗНЪНЕФШЫЪ§ЫљдкЩШаЮдВаФНЧЕФЖШЪ§ЮЊЃК
жжЗНЪНЕФШЫЪ§ЫљдкЩШаЮдВаФНЧЕФЖШЪ§ЮЊЃК![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃК![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉИљОнЬтвтСаБэШчЯТЃК
Фа | Фа | Фа | ХЎ | ХЎ | |
Фа | (Фа1ЃЌФа2) | (Фа1ЃЌФа3) | (Фа1ЃЌХЎ1) | (Фа1ЃЌХЎ2) | |
Фа | (Фа2ЃЌФа1) | (Фа2ЃЌФа3) | (Фа2ЃЌХЎ1) | (Фа2ЃЌХЎ2) | |
Фа | (Фа3ЃЌФа1) | (Фа3ЃЌФа2) | (Фа3ЃЌХЎ1) | (Фа3ЃЌХЎ2) | |
ХЎ | (ХЎ1ЃЌФа1) | (ХЎ1ЃЌФа2) | (ХЎ1ЃЌФа3) | (ХЎ1ЃЌХЎ2) | |
ХЎ | (ХЎ2ЃЌФа1) | (ХЎ2ЃЌФа2) | (ХЎ2ЃЌФа3) | (ХЎ2ЃЌХЎ1) |
гЩЩЯБэПЩжЊЃЌЙВга![]() жжЕШПЩФмЕФНсЙћЃЌЦфжаЧЁКУГщЕН
жжЕШПЩФмЕФНсЙћЃЌЦфжаЧЁКУГщЕН![]() Фа
Фа![]() ХЎЕФНсЙћга
ХЎЕФНсЙћга![]() жжЃЌ
жжЃЌ
ЁрЧЁКУГщЕН![]() Фа
Фа![]() ХЎЕФИХТЪЮЊЃК
ХЎЕФИХТЪЮЊЃК![]() ЃЎ
ЃЎ


 жаПМНтЖСПМЕуОЋСЗЯЕСаД№АИ
жаПМНтЖСПМЕуОЋСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
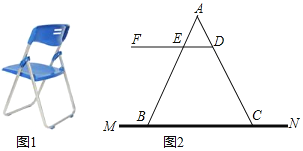
ЁОЬтФПЁПШчЭМ1ЪЧвЛжжелЕўвЮЃЌКіТдЦфжЇМмЕШЕФПэЖШЃЌЕУЕНЫћЕФВрУцМђЛЏНсЙЙЭМ![]() ЭМ
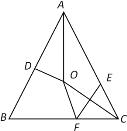
ЭМ![]() ЃЌжЇМмгызјАхОљгУЯпЖЮБэЪОЃЌШєзљАхDFЦНаагкЕиУцMNЃЌЧАжЇГХМмABгыКѓжЇГХМмACЗжБ№гызљАхDFНЛгкЕуEЁЂDЃЌЯжВтЕУ
ЃЌжЇМмгызјАхОљгУЯпЖЮБэЪОЃЌШєзљАхDFЦНаагкЕиУцMNЃЌЧАжЇГХМмABгыКѓжЇГХМмACЗжБ№гызљАхDFНЛгкЕуEЁЂDЃЌЯжВтЕУ![]() РхУзЃЌ
РхУзЃЌ ![]() РхУзЃЌ
РхУзЃЌ ![]() ЃЎ
ЃЎ
![]() ЧѓвЮзгЕФИпЖШ
ЧѓвЮзгЕФИпЖШ![]() МДвЮзгЕФзљАхDFгыЕиУцMNжЎМфЕФОрРы
МДвЮзгЕФзљАхDFгыЕиУцMNжЎМфЕФОрРы![]() ОЋШЗЕН1РхУз
ОЋШЗЕН1РхУз![]()
![]() ЧѓвЮзгСННХBЁЂCжЎМфЕФОрРы
ЧѓвЮзгСННХBЁЂCжЎМфЕФОрРы![]() ОЋШЗЕН1РхУз
ОЋШЗЕН1РхУз![]() ВЮПМЪ§ОнЃК
ВЮПМЪ§ОнЃК ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABCDЕФЖдНЧЯпACЁЂBDНЛгкЕуOЃЌAEЦНЗжЁЯBADНЛBCгкЕуEЃЌЧвЁЯADC=60ЁуЃЌAB=![]() BCЃЌСЌНгOEЃЎЯТСаНсТлЃКЂйЁЯCAD=30ЁуЃЛЂкSABCD=ABACЃЛЂлOB=ABЃЛЂмOE=
BCЃЌСЌНгOEЃЎЯТСаНсТлЃКЂйЁЯCAD=30ЁуЃЛЂкSABCD=ABACЃЛЂлOB=ABЃЛЂмOE=![]() BCЃЌГЩСЂЕФИіЪ§гаЃЈЁЁЁЁЃЉ
BCЃЌГЩСЂЕФИіЪ§гаЃЈЁЁЁЁЃЉ

A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпОЙ§AЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ5ЃЌ0ЃЉЃЌCЃЈ0ЃЌ![]() ЃЉШ§ЕуЃЎ
ЃЉШ§ЕуЃЎ

ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯгавЛЕуPЃЌЪЙPA+PCЕФжЕзюаЁЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЕуMЮЊxжсЩЯвЛЖЏЕуЃЌдкХзЮяЯпЩЯЪЧЗёДцдквЛЕуNЃЌЪЙвдAЃЌCЃЌMЃЌNЫФЕуЙЙГЩЕФЫФБпаЮЮЊЦНааЫФБпаЮЃПШєДцдкЃЌЧѓЕуNЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌEЁЂFЗжБ№дкODЁЂOCЩЯЃЌЧвDE=CFЃЌСЌНгDFЁЂAEЃЌAEЕФбгГЄЯпНЛDFгкЕуMЃЎ
ЃЈ1ЃЉЧѓжЄЃКAE=DFЃЛ
ЃЈ2ЃЉЧѓжЄЃКAMЁЭDFЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌАДвдЯТВНжшзїЭМЃКЂйЗжБ№вдAЁЂBЮЊдВаФЃЌДѓгк![]() ABЕФГЄЮЊАыОЖЛЛЁЃЌСНЛЁЯрНЛгкЕуMЁЂNЃЛЂкзїжБЯпMNНЛACгкЕуDЃЌСЌНгBDЃЎШєCD=CBЃЌЁЯA=35ЁуЃЌдђЁЯCЕШгкЃЈ ЃЉ
ABЕФГЄЮЊАыОЖЛЛЁЃЌСНЛЁЯрНЛгкЕуMЁЂNЃЛЂкзїжБЯпMNНЛACгкЕуDЃЌСЌНгBDЃЎШєCD=CBЃЌЁЯA=35ЁуЃЌдђЁЯCЕШгкЃЈ ЃЉ

A. 40Ёу B. 50Ёу C. 60Ёу D. 70Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫТфЪЕЕГЕФЁАОЋзМЗіЦЖЁБеўВпЃЌAЁЂBСНГЧОіЖЈЯђCЁЂDСНЯчдЫЫЭЗЪСЯвджЇГжХЉДхЩњВњЃЌвбжЊAЁЂBСНГЧЙВгаЗЪСЯ500ЖжЃЌЦфжаAГЧЗЪСЯБШBГЧЩй100ЖжЃЌДгAГЧЭљCЁЂDСНЯчдЫЗЪСЯЕФЗбгУЗжБ№ЮЊ20дЊ/ЖжКЭ25дЊ/ЖжЃЛДгBГЧЭљCЁЂDСНЯчдЫЗЪСЯЕФЗбгУЗжБ№ЮЊ15дЊ/ЖжКЭ24дЊ/ЖжЃЎЯжCЯчашвЊЗЪСЯ240ЖжЃЌDЯчашвЊЗЪСЯ260ЖжЃЎ
ЃЈ1ЃЉAГЧКЭBГЧИїгаЖрЩйЖжЗЪСЯЃП
ЃЈ2ЃЉЩшДгAГЧдЫЭљCЯчЗЪСЯxЖжЃЌзмдЫЗбЮЊyдЊЃЌЧѓГізюЩйзмдЫЗбЃЎ
ЃЈ3ЃЉгЩгкИќЛЛГЕаЭЃЌЪЙAГЧдЫЭљCЯчЕФдЫЗбУПЖжМѕЩйaЃЈ0ЃМaЃМ6ЃЉдЊЃЌетЪБдѕбљЕїдЫВХФмЪЙзмдЫЗбзюЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌМКжЊ![]() ЃЌвд
ЃЌвд![]() ЮЊжБОЖЕФ
ЮЊжБОЖЕФ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌЕу
ЃЌЕу![]() ЮЊЛЁ
ЮЊЛЁ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЎЧв
ЃЎЧв![]() ЃЎ
ЃЎ
(1)ЧѓжЄЃК![]() ЪЧ
ЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
(2)Шє![]() ЕФАыОЖЮЊ4ЃЌ
ЕФАыОЖЮЊ4ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
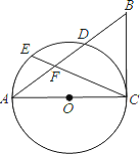
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌ![]() ЃЌAOЪЧЁЯBACЕФЦНЗжЯпЃЌгыABЕФДЙжБЦНЗжЯпDOНЛгкЕуOЃЌЁЯACBбиEFелЕўКѓЃЌЕуC ИеКУгыЕуOжиКЯЃЎЯТСаНсТлДэЮѓЕФЪЧЃЈ ЃЉ
ЃЌAOЪЧЁЯBACЕФЦНЗжЯпЃЌгыABЕФДЙжБЦНЗжЯпDOНЛгкЕуOЃЌЁЯACBбиEFелЕўКѓЃЌЕуC ИеКУгыЕуOжиКЯЃЎЯТСаНсТлДэЮѓЕФЪЧЃЈ ЃЉ
A.AOЃНCOB.ЁЯECOЃНЁЯFCOC.EFЁЭOCD.ЁЯBFOЃН2ЁЯFOC
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com