
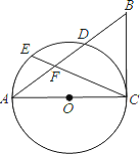
【题目】如图,己知![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为弧
为弧![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() .且
.且![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 的半径为4,
的半径为4,![]() ,求
,求![]() 的长.
的长.
科目:初中数学 来源: 题型:
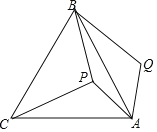
【题目】如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60得到线段AQ,连接BQ,若PA=3,PB=4,PC=5,则四边形APBQ的面积为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市将举办“时代新人说”第三季,幸福园小区居委会为了解居民获取“时代新人说”活动相关信息的方式进行了随机抽样调查,调查设置了A(网络),B(电视),C(报纸),D(其他)四种方式,被调查的居民只能从中选取一种方式,并根据收集到的数据绘制了如下的两幅均不完整的统计图:
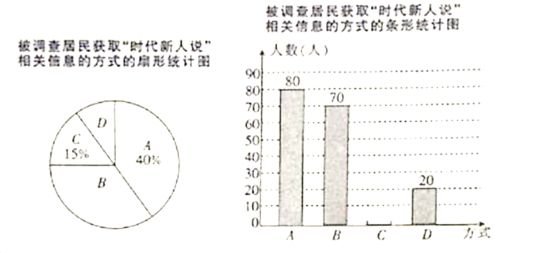
根据图中信息,解答下列问题.
![]() 补全上面的条形统计图.
补全上面的条形统计图.
![]() 在扇形统计图中,选择
在扇形统计图中,选择![]() 种方式的人数所占的百分比是 ,选择
种方式的人数所占的百分比是 ,选择![]() 种方式的人数所在扇形圆心角的度数是 .
种方式的人数所在扇形圆心角的度数是 .
![]() 该小区有
该小区有![]() 男
男![]() 女报名了社区的“时代新人说”活动,由于人数限制,居委会只能从中随机抽取
女报名了社区的“时代新人说”活动,由于人数限制,居委会只能从中随机抽取![]() 名参加活动,请你用画树状图或列表的方法求出恰好抽到
名参加活动,请你用画树状图或列表的方法求出恰好抽到![]() 男
男![]() 女的概率.
女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条结论:你认为其中正确结论的个数有( )
(1)a<0;(2)b>0;(3)a﹣b+c>0;(4)2a+b<0.
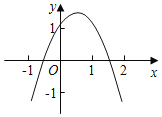
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=10cm,E为对角线BD上一动点,连接AE,CE,过E点作EF⊥AE,交直线BC于点F.E点从B点出发,沿着BD方向以每秒2cm的速度运动,当点E与点D重合时,运动停止.设△BEF的面积为ycm2,E点的运动时间为x秒.
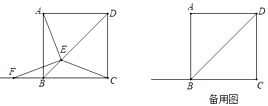
(1)求证:CE=EF;
(2)求y与x之间关系的函数表达式,并写出自变量x的取值范围;
(3)求△BEF面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面内的点![]() 和点
和点![]() ,给出如下定义:点
,给出如下定义:点![]() 为平面内一点,若点
为平面内一点,若点![]() 使得
使得![]() 是以
是以![]() 为顶角且
为顶角且![]() 小于90°的等腰三角形,则称点
小于90°的等腰三角形,则称点![]() 是点
是点![]() 关于点
关于点![]() 的锐角等腰点.如图,点
的锐角等腰点.如图,点![]() 是点
是点![]() 关于点
关于点![]() 的锐角等腰点.
的锐角等腰点.
在平面直角坐标系xOy中,点O为坐标原点
(1)已知点![]() ,在点
,在点![]() ,
,![]() ,
,![]() ,
,![]() 中,是点
中,是点![]() 关于点
关于点![]() 的锐角等腰点的是 ;
的锐角等腰点的是 ;
(2)已知点![]() ,点
,点![]() 在直线
在直线![]() 上,若点
上,若点![]() 是点
是点![]() 关于点
关于点![]() 的锐角等腰点,求实数
的锐角等腰点,求实数![]() 的取值范围.
的取值范围.
(3) 点![]() 是
是![]() 轴上的动点,
轴上的动点,![]() ,
,![]() ,点
,点![]() 是以点
是以点![]() 为圆心,2为半径的圆上一动点.且满足
为圆心,2为半径的圆上一动点.且满足![]() ,若直线
,若直线![]() 上存在点
上存在点![]() 关于点
关于点![]() 的锐角等腰点,请直接写出
的锐角等腰点,请直接写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钟南山院士在谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷(满分100分),社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据
甲小区:80 85 90 95 90 95 90 65 75 100 90 70 95 90 80 80 90 95 60 100
乙小区:60 80 95 80 90 65 80 85 85 100 80 95 90 80 90 70 80 90 75 100
整理数据
成绩 小区 |
|
|
|
|
甲小区 |
|
|
|
|
乙小区 |
|
|
|
|
分析数据
数据名称 计量小区 | 平均数 | 中位数 | 众数 |
甲小区 |
|
|
|
乙小区 |
|
|
|
应用数据
(1)填空:![]() =______,
=______,![]() =______;
=______;
(2)若乙小区共有1200人参与答卷,请估计乙小区成绩大于90分的人数;
(3)社区管理人员看完统计数据,认为甲小区对新型冠状病毒肺炎防护知识掌握更好,请你写出社区管理人员的理由;为了更好地宣传新型冠状病毒肺炎防护知识,社区管理人员决定从甲、乙小区的4个满分试卷中随机抽取两份试卷对小区居民进行网络宣传讲解培训,请用列表格或画树状图的方法求出甲、乙小区各抽到一份满分试卷的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在离水面高度(AC)为2米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米的速度收绳子.
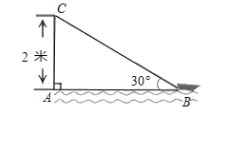
问:(1)未开始收绳子的时候,图中绳子BC的长度是多少米?
(2)收绳2秒后船离岸边多少米?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一直角三角形纸片,∠C=90°,BC=6,AC=8,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长为( )
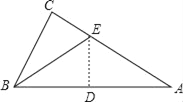
A. 2![]() B.
B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com