
【题目】如图1,点![]() 是线段
是线段![]() 的中点,分别以
的中点,分别以![]() 和
和![]() 为边在线段
为边在线段![]() 的同侧作等边三角形
的同侧作等边三角形![]() 和等边三角形
和等边三角形![]() ,连结
,连结![]() 和
和![]() ,相交于点
,相交于点![]() ,连结
,连结![]() ,
,
(1)求证:![]() ;
;
(2)求![]() 的大小;
的大小;
(3)如图2,![]() 固定不动,保持
固定不动,保持![]() 的形状和大小不变,将
的形状和大小不变,将![]() 绕着点
绕着点![]() 旋转(
旋转(![]() 和
和![]() 不能重叠),求
不能重叠),求![]() 的大小.
的大小.
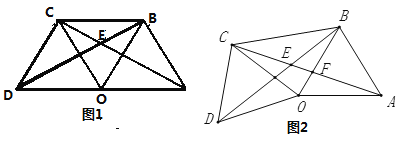
【答案】(1)证明见解析;(2)∠AEB=60°;(3)∠AEB=60°.
【解析】
(1)由等边三角形的性质可得![]() ,
,![]() ,继而可得∠AOC=∠DOB,利用SAS证明
,继而可得∠AOC=∠DOB,利用SAS证明![]() ,利用全等三角形的性质即可得;;
,利用全等三角形的性质即可得;;
(2)先证明![]() ,从而可得 ∠ODB=∠DBO,再利用三角形外角的性质可求得
,从而可得 ∠ODB=∠DBO,再利用三角形外角的性质可求得![]() ,
,![]() ,进而根据
,进而根据![]() 即可求得答案;
即可求得答案;
(3)证明![]() ,从而可得
,从而可得![]() ,再由
,再由![]() ,可得
,可得![]() ,设
,设![]() 与
与![]() 交于点
交于点![]() ,利用三角形内角和定理以及对顶角的性质即可求得
,利用三角形内角和定理以及对顶角的性质即可求得![]() .
.
(1)∵![]() 和
和![]() 均为等边三角形,
均为等边三角形,
∴![]() ,
,![]() ,
,
∴![]()
![]() ,
,
即∠AOC=∠DOB,
∴![]() (SAS)
(SAS)
∴![]() ;
;
(2)∵O为AD中点,
∴DO=AO,
∵OA=OB,
∴![]() ,
,
∴∠ODB=∠DBO,
∵∠ODB+∠DBO=∠AOB=60°,
∴![]()
同理,![]() ,
,
∴![]() ;
;
(3)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵CO=DO,AO=BO,AO=DO,
∴OC=OB,
∴![]() (SAS),
(SAS),
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() 与
与![]() 交于点
交于点![]() ,
,
∵![]() ,
,![]() ,
,
又![]() ,
,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
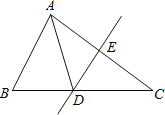
【题目】如图,在△ABC中,AC的垂直平分线交BC于D,交AC于E,AE=3cm, △ABD的周长为13cm,那么△ABC的周长为_______________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=3cm,BC=5cm;,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DE+DF的长度为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年3月,某集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
评估成绩 | 评定等级 | 频数 |
| A | 2 |
| B | b |
| C | 15 |
| D | 6 |
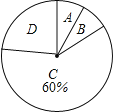
根据以上信息解答下列问题:
(1)求m,b的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;
(3)从评估成绩不少于80分的连锁店中,任选2家介绍营销经验,用树状图或列表法求其中至少有一家是A等级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是直线AB,DE之间的一点,∠ACD=90°,下列条件能使得AB∥DE的是( )
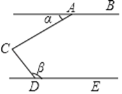
A. ∠α+∠β=180° B. ∠β﹣∠α=90° C. ∠β=3∠α D. ∠α+∠β=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),![]() ,
,![]() ,
,![]() 垂足分别为
垂足分别为![]() 、
、![]() ,
,![]() .点
.点![]() 在线段
在线段![]() 上以
上以![]() 的速度由点
的速度由点![]() 向点
向点![]() 运动,同时点
运动,同时点![]() 在射线
在射线![]() 上运动.它们运动的时间为
上运动.它们运动的时间为![]() (当点
(当点![]() 运动结束时,点
运动结束时,点![]() 运动随之结束).
运动随之结束).
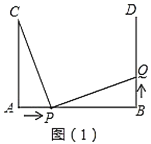
(1)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,当
的运动速度相等,当![]() 时,
时,![]() 与
与![]() 是否全等,并判断此时线段
是否全等,并判断此时线段![]() 和线段
和线段![]() 的位置关系,请分别说明理由;
的位置关系,请分别说明理由;
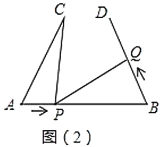
(2)如图(2),若“![]() ,
,![]() ”改为“
”改为“![]() ”,点
”,点![]() 的运动速度为
的运动速度为![]() ,其它条件不变,当点
,其它条件不变,当点![]() 、
、![]() 运动到何处时有
运动到何处时有![]() 与
与![]() 全等,求出相应的
全等,求出相应的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数y=ax2+bx+c的图象有下列命题,其中是假命题的个数是( )
①当c=0时,函数的图象经过原点;
②当b=0时,函数的图象关于y轴对称;
③函数的图象最高点的纵坐标是![]() ;
;
④当c>0且函数的图象开口向下时,方程ax2+bx+c=0必有两个不相等的实根.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com