
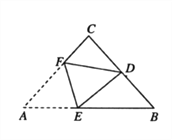
【题目】如图,在等腰直角![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,
重合,![]() 为折痕,则
为折痕,则![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】先根据翻折变换的性质得到△DEF≌△AEF,再根据等腰三角形的性质及三角形外角的性质可得到∠BED=CDF,设CD=1,CF=x,则CA=CB=2,再根据勾股定理即可求出x的值,利用三角函数的定义求出sin∠BED=sin∠CDF的值.
∵△DEF是△AEF翻折而成,
∴△DEF≌△AEF,
∴∠A=∠EDF,DF=FA,
∵△ABC是等腰直角三角形,
∴∠EDF=45°,由三角形外角性质得∠CDF+45°=∠BED+45°,
∴∠BED=∠CDF,
设CD=1,CF=x,则CA=CB=2,
∴DF=FA=2-x,
∴在Rt△CDF中,由勾股定理得,CF2+CD2=DF2,即x2+1=(2-x)2,
解得x=![]() ,
,
∴sin∠BED=sin∠CDF=![]() .
.
故选B.


科目:初中数学 来源: 题型:
【题目】已知,如图点A(1,1),B(2,﹣3),点P为x轴上一点,当|PA﹣PB|最大时,点P的坐标为( )

A. (﹣1,0) B. (![]() ,0) C. (
,0) C. (![]() ,0) D. (1,0)
,0) D. (1,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
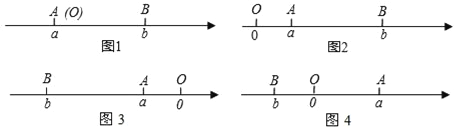
【题目】阅读下面材料:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|,当A、B两点都不在原点时.
(1)如图2,点A、B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=a﹣b=|a﹣b|
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=a﹣b=|a﹣b|
综上,数轴上A、B两点的距离|AB|=|a﹣b|
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示﹣2和5的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2那么x为 .
(3)若x表示一个有理数,则|x﹣1|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如图所示
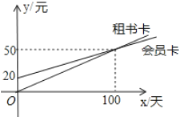
(1)分别写出用租书卡和会员卡租书的金额y(元)与租书时间x(天)之间的函数表达式;
(2)若租150天,使用哪种租书卡更便宜?便宜多少?
(3)请写出使用租书卡更合算的租书时间的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车油箱现有汽油50L,如果不再加油,那么油箱中的油量![]() (L)随行驶里程
(L)随行驶里程![]() (km)的增加而减少,平均耗油量为0.11L/km.
(km)的增加而减少,平均耗油量为0.11L/km.
(1)写出表示![]() 与
与![]() 的函数关系式.
的函数关系式.
(2)指出自变量![]() 的取值范围.
的取值范围.
(3)汽车行驶200km时,油箱中还有多少汽油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图l,在![]() 中,点
中,点![]() ,
,![]() 分别在边
分别在边![]() 和
和![]() 上,点
上,点![]() ,
,![]() 在对角线
在对角线![]() 上,且
上,且![]() ,
,![]() .
.
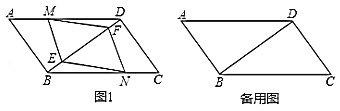
(1)求证:四边形![]() 是平行四边形:
是平行四边形:
(2)若![]() ,
,![]() ,
,![]() .
.
①当四边形![]() 是菱形时,
是菱形时,![]() 的长为______;
的长为______;
②当四边形![]() 是正方形时,
是正方形时,![]() 的长为______;
的长为______;
③当四边形![]() 是矩形且
是矩形且![]() 时,
时,![]() 的长为______.
的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成下列各小题.
(1)先化简,再求值:![]() ,其中
,其中![]() 是最大的负整数,
是最大的负整数,![]() 是2的倒数;
是2的倒数;
(2)已知关于![]() 的方程
的方程![]() 与方程
与方程![]() 的解相同,求
的解相同,求![]() 的值;
的值;
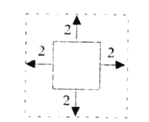
(3)用一根长为![]() (单位:
(单位:![]() )的铁丝,首尾相接围成一个正方形,要将它按如图所示的方式向外等距扩
)的铁丝,首尾相接围成一个正方形,要将它按如图所示的方式向外等距扩![]() ,得到新的正方形,求这根铁丝增加的长度.
,得到新的正方形,求这根铁丝增加的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com