
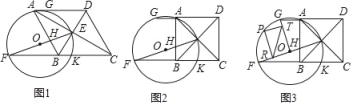
【题目】已知四边形ABCD是菱形,AC、BD交于点E,点F在CB的延长线上,连结EF交AB于H,以EF为直径作⊙O,交直线AD于A、G两点,交BC于K点.
(1)如图1,连结AF,求证:四边形AFBD是平行四边形;
(2)如图2,当∠ABC=90°时,求tan∠EFC的值;
(3)如图3,在(2)的条件下,连结OG,点P在弧FG上,过点P作PT∥OF交OG于T,PR∥OG交OF于R点,连结TR,若AG=2,在点P运动过程中,探究线段TR的长是否为定值,如果是,则求出这个定值;如果不是,请说明理由.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)连接AF,由EF是⊙O的直径知FA⊥AC,由四边形ABCD是菱形知BD⊥AC、AD∥FB,据此可得FA∥BD,即可得证;
(2)连接EK,先证四边形ABCD是正方形,由EF是⊙O的直径知FK⊥EK,设BK=EK=a,则BC=AD=FB=2a,根据tan∠EFC=![]() 可得答案;
可得答案;
(3)连接OP、FA,过点O作OM⊥GD,并延长MO交FC于点N,先证四边形PROT是矩形得RT=OP=OG,由MN⊥FC知tan∠EFC=tan∠GOM=![]() ,由AG=2、OM⊥GD知GM=1、OM=3,由勾股定理可得GO=
,由AG=2、OM⊥GD知GM=1、OM=3,由勾股定理可得GO=![]() ,继而可得答案.
,继而可得答案.
(1)如图1,连接AF,

∵EF是⊙O的直径,
∴∠FAC=90°,即FA⊥AC,
∵四边形ABCD是菱形,
∴BD⊥AC,AD∥BC、即AD∥FB,
∴FA∥BD,
∴四边形AFBD是平行四边形;
(2)如图2,连接EK,
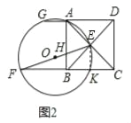
∵∠ABC=90°,四边形ABCD是菱形,
∴四边形ABCD是正方形,
∵EF是⊙O的直径,
∴FK⊥EK,
设BK=EK=a,则BC=AD=FB=2a,
则tan∠EFC=![]() =
=![]() ;
;
(3)TR的长是定值,
如图3,连接OP、FA,过点O作OM⊥GD,并延长MO交FC于点N,

∵EF是⊙O的直径,
∴FA⊥EA,
又∵四边形ABCD是正方形,
∴∠BAC=45°,
∴∠GAF=45°,
∴∠GOF=90°,
∵PT∥OF、PR∥OG,
∴四边形PROT是矩形,
∴RT=OP=OG,
∵OM⊥GD、GD∥FC,
∴MN⊥FC,
∴tan∠EFC=tan∠GOM=![]() ,
,
∵AG=2、OM⊥GD,
∴GM=1,
∴OM=3,
由勾股定理可得GO=![]() ,
,
∴RT=![]() .
.


科目:初中数学 来源: 题型:
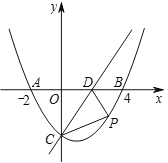
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与直线
,与直线![]() 交于点
交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求该抛物线的解析式.
(2)点![]() 是抛物线上第四象限上的一个动点,连接
是抛物线上第四象限上的一个动点,连接![]() ,
,![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标.
的坐标.
(3)将抛物线的对称轴向左平移3个长度单位得到直线![]() ,点
,点![]() 是直线
是直线![]() 上一点,连接
上一点,连接![]() ,
,![]() ,若直线
,若直线![]() 上存在使
上存在使![]() 最大的点
最大的点![]() ,请直接写出满足条件的点
,请直接写出满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生200米跑的水平,从中随机抽取部分男生进行测试,并把测试成绩分为D、C、B、A四个等次绘制成如图所示的不完整的统计图,请你依图解答下列问题:
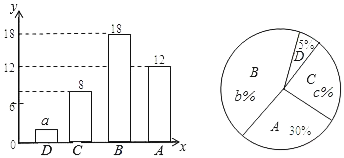
(1)a= ,b= ,c= ;
(2)扇形统计图中表示C等次的扇形所对的圆心角的度数为 度;
(3)学校决定从A等次的甲、乙、丙、丁四名男生中,随机选取两名男生参加全市中学生200米跑比赛,请用列表法或画树状图法,求甲、乙两名男生同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
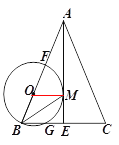
【题目】如图,在△ABC中,AB=AC,AE是BC边上的高线,BM平分∠ABC交AE于点M,经过B,M 两点的⊙O交BC于点G,交AB于点F ,FB为⊙O的直径.
(1)求证:AM是⊙O的切线
(2)当BE=3,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
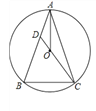
【题目】如图,△ABC内接于⊙O,AB=AC,CO的延长线交AB于点D.
(1)求证:AO平分∠BAC;
(2)若BC=6,sin∠BAC=![]() ,求AC和CD的长.
,求AC和CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
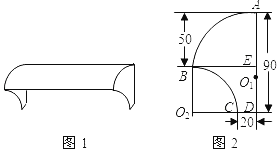
【题目】小帅家的新房子刚装修完,便遇到罕见的大雨,于是他向爸爸提议给窗户安上遮雨罩.如图1所示的是他了解的一款雨罩.它的侧面如图2所示,其中顶部圆弧AB的圆心O在整直边缘D上,另一条圆弧BC的圆心O.在水平边缘DC的廷长线上,其圆心角为90°,BE⊥AD于点E,则根据所标示的尺寸(单位:c)可求出弧AB所在圆的半径AO的长度为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题:
(1)本次调查属于 调查,样本容量是 ;
(2)请补全频数分布直方图中空缺的部分;
(3)求这50名学生每周课外体育活动时间的平均数;
(4)估计全校学生每周课外体育活动时间不少于6小时的人数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com