
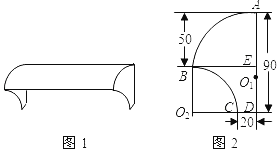
【题目】小帅家的新房子刚装修完,便遇到罕见的大雨,于是他向爸爸提议给窗户安上遮雨罩.如图1所示的是他了解的一款雨罩.它的侧面如图2所示,其中顶部圆弧AB的圆心O在整直边缘D上,另一条圆弧BC的圆心O.在水平边缘DC的廷长线上,其圆心角为90°,BE⊥AD于点E,则根据所标示的尺寸(单位:c)可求出弧AB所在圆的半径AO的长度为_____cm.
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
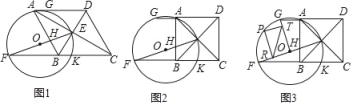
【题目】已知四边形ABCD是菱形,AC、BD交于点E,点F在CB的延长线上,连结EF交AB于H,以EF为直径作⊙O,交直线AD于A、G两点,交BC于K点.
(1)如图1,连结AF,求证:四边形AFBD是平行四边形;
(2)如图2,当∠ABC=90°时,求tan∠EFC的值;
(3)如图3,在(2)的条件下,连结OG,点P在弧FG上,过点P作PT∥OF交OG于T,PR∥OG交OF于R点,连结TR,若AG=2,在点P运动过程中,探究线段TR的长是否为定值,如果是,则求出这个定值;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
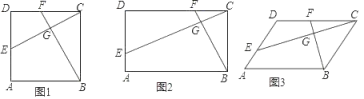
【题目】(1)如图1,正方形ABCD中,E、F分别是AD、DC边上的点,CE与BF交于点G,BF⊥CE,求证:BF=CE;
(2)如图2,矩形ABCD中,AB=2AD,E、F分别是AD、DC边上的点,CE与BF交于点G,∠A+∠BGE=180°,求证:CE=2BF;
(3)如图3,若(2)中的四边形ABCD是平行四边形,且∠A<90°,则CE=2BF是否仍然成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
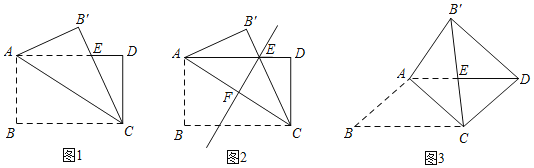
【题目】课题学习:矩形折纸中的数学实践操作:折纸不仅是一项有趣的活动,也是一项益智的数学活动.数学课上,老师给出这样一道题将矩形纸片ABCD沿对角线AC翻折,使点B落在矩形所在平面内,B'C和AD相交于点E,如图1所示.
探素发现:
(1)在图1中,①请猜想并证明AE和EC的数量关系;②连接B'D,请猜想并证明B'D和AC的位置关系;
(2)第1小组的同学发现,图1中,将矩形ABCD沿对角线AC翻折所得到的图形是轴对称图形.若沿对称轴EF再次翻折所得到的图形仍是轴对称图形,展开后如图2所示,请你直接写出该矩形纸片的长、宽之比;
(3)若将图1中的矩形变为平行四边形时(AB≠BC),如图3所示,(1)中的结论①和结论②是否仍然成立,请直接写出你的判断.
拓展应用:
(4)在图3中,若∠B=30°,AB=2,请您直接写出:当BC的长度为多少时,△AB'D恰好为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
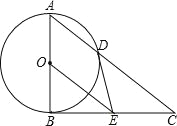
【题目】如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心、OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=2CD·OE;
(3)若cos∠BAD=![]() ,BE=6,求OE的长.
,BE=6,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
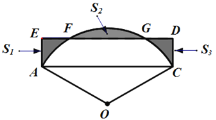
【题目】如图,半径为3的扇形AOB,∠AOB=120°,以AB为边作矩形ABCD交弧AB于点E,F,且点E,F为弧AB的四等分点,矩形ABCD与弧AB形成如图所示的三个阴影区域,其面积分别为![]() ,
,![]() ,
,![]() ,则
,则![]() 为( )(
为( )(![]() 取
取![]() )
)
A. ![]()
![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com