
【题目】设AD为∠BAC的平分线,AB=8,AC=10,AD=6,E为AC上一点,AE=2,M为AE的中点,N为BC的中点,则MN=( )
A.5B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
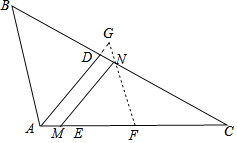
如图,取AC的中点F,连接FN,延长FN、AC交于点G,先利用三角形的中位线定理证得FN∥AB并求得FN的值;再证明△DGN∽△DAB,列出比例式求得DG的值,则AG的值可求;然后证明△NFM∽△GFA,列出比例式即可求得MN的值.
如图,取AC的中点F,连接FN,延长FN、AC交于点G
∵AE=2,M为AE的中点,
∴AM=1
∵AF=![]() AC=5,
AC=5,
∴FM=5﹣1=4
∵AF=CF,BN=CN
∴FN∥AB,FN=![]() AB=
AB=![]() ×8=4=FM
×8=4=FM
∴∠G=∠BAG
又∠BAG=∠CAG
∴∠G=∠CAG
∴AF=GF=5
∵FN∥AB
∴△DGN∽△DAB
∴![]() =
=![]()
∵AD=6,GN=FG﹣FN=5﹣4=1,AB=8
∴![]() =
=![]()
∴DG=![]()
∵![]() =
=![]() =
=![]() ,∠NFM=∠GFA
,∠NFM=∠GFA
∴△NFM∽△GFA
∴![]() =
=![]() =
=![]() =
=![]()
∴![]()
故选:C.


科目:初中数学 来源: 题型:
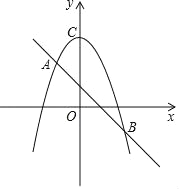
【题目】如图,一次函数y=kx+b的图象与二次函数y=﹣x2+c的图象相交于A(﹣1,2),B(2,n)两点.
(1)求一次函数和二次函数的解析式;
(2)根据图象直接写出使二次函数的值大于一次函数的值的x的取值范围;
(3)设二次函数y=﹣x2+c的图象与y轴相交于点C,连接AC,BC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等的凸四边形叫做“准菱形”.利用该定义完成以下各题:
(1) 理解
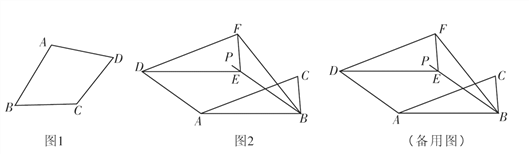
填空:如图1,在四边形ABCD中,若 (填一种情况),则四边形ABCD是“准菱形”;
(2)应用
证明:对角线相等且互相平分的“准菱形”是正方形;(请画出图形,写出已知,求证并证明)
(3) 拓展
如图2,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BP方向平移得到△DEF,连接AD,BF,若平移后的四边形ABFD是“准菱形”,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x 学校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:
这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分 | 中位数 | 众数 |
甲 | 74.2 | n | 5 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x 学校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:
这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分 | 中位数 | 众数 |
甲 | 74.2 | n | 5 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AH是⊙O的直径,点E,F分别在矩形ABCD的边BC和CD上,B为直径OH上一点,AE平分∠FAH交⊙O于点E,过点E的直线FG⊥AF,垂足为F.
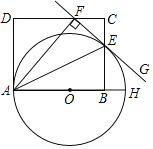
(1)求证:直线FG是⊙O的切线;
(2)若AD=8,EB=5,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
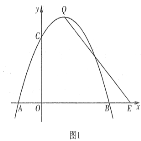
【题目】如图1,在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 过抛物线的顶点
过抛物线的顶点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
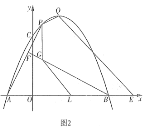
(2)如图2,点![]() 在点
在点![]() 和点
和点![]() 之间的抛物线上,连接
之间的抛物线上,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 右侧的
右侧的![]() 轴上,连接
轴上,连接![]() ,且
,且![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
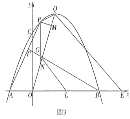
(3)如图3,在(2)的条件下,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
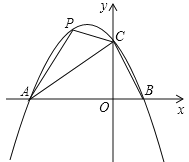
(1)求这个二次函数的解析式;
(2)点![]() 是直线
是直线![]() 上方的抛物线上一动点,是否存在点
上方的抛物线上一动点,是否存在点![]() ,使得
,使得![]() 的面积最大?若存在,求出点
的面积最大?若存在,求出点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(3)点![]() 是直线
是直线![]() 上方的抛物线上一动点,过点
上方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() .是否存在点
.是否存在点![]() ,使以点
,使以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,直接写出点
相似?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张同学学完统计知识后,随机调查了她所在辖区若干名居民的年龄,将调查数据绘制成如下扇形统计图和条形统计图:


请根据以上不完整的统计图提供的信息,解答下列问题:
(1)小张同学共调查了_____名居民的年龄,扇形统计图中a=_____;
(2)补全条形统计图,并注明人数;
(3)若在该辖区中随机抽取一人,那么这个人年龄是60岁及以上的概率为_____;
(4)若该辖区年龄在0~14岁的居民约有3500人,请估计该辖区居民人数是_____人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com