
【题目】如图,AH是⊙O的直径,点E,F分别在矩形ABCD的边BC和CD上,B为直径OH上一点,AE平分∠FAH交⊙O于点E,过点E的直线FG⊥AF,垂足为F.
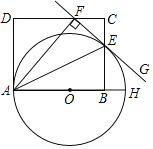
(1)求证:直线FG是⊙O的切线;
(2)若AD=8,EB=5,求⊙O的直径.
【答案】(1)见解析;(2)⊙O的直径为![]() .
.
【解析】
(1)根据角平分线和半径相等,得∠OEA=∠EAF,推得OE∥AF,进而根据切线的判定即可证明;
(2)先证明Rt△ABE≌Rt△AFE,得AF=AB,再根据勾股定理即可求得半径的长,进而求得直径的长.
(1)如图,连接OE,
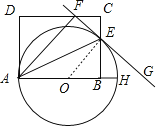
∵OA=OE,
∴∠OAE=∠OEA,
∵AE平分∠FAH,
∴∠OAE=∠FAE,
∴∠OEA=∠FAE,
∴OE∥AF,
∴∠AFE+∠OEF∠=180°,
∵AF⊥GF,
∴∠AFE=90°,
∴∠OEF=90°,
∴OE⊥GF,
∵点E在圆上,OE是半径,
∴GF是⊙O的切线;
(2)设AB=x,
∵四边形ABCD是矩形,
∴AB=CD=x,BC=AD=8,
∴CE=BC﹣BE=3,
∵AE是∠BAF的角平分线,BE⊥AB,EF⊥AF,
∴EF=BE=5,
在Rt△CEF中,根据勾股定理,得CF=4,
∴DF=CD﹣CF=x﹣4,
AE=AE,
∴Rt△ABE≌Rt△AFE(HL),
∴AF=AB=x,
在Rt△ADF中,x2﹣(x﹣4)2=64,
∴x=10,
∴AB=10,
设⊙O的半径为r,
∴OB=10﹣r,
在Rt△BOE中,r2=(10﹣r)2+25,
∴r=![]() ,
,
答:⊙O的直径为![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④b2-4ac>0;其中正确的结论有________(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,点F在BC边上,过A,B,F三点的⊙O交AC于另一点D,作直径AE,连结EF并延长交AC于点G,连结BE,BD,四边形BDGE是平行四边形.
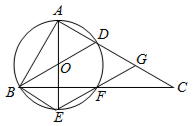
(1)求证:AB=BF.
(2)当F为BC的中点,且AC=3时,求⊙O的直径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图,则下列判断错误的是( ).

A. 甲的数学成绩高于班级平均分,且成绩比较稳定
B. 乙的数学成绩在班级平均分附近波动,且比丙好
C. 丙的数学成绩低于班级平均分,但成绩逐次提高
D. 就甲、乙、丙三个人而言,乙的数学成绩最不稳
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设AD为∠BAC的平分线,AB=8,AC=10,AD=6,E为AC上一点,AE=2,M为AE的中点,N为BC的中点,则MN=( )
A.5B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了帮助遭受自然灾害的地区,某学校号召同学们自愿捐款,已知第一次捐款总额为5800元,第二次捐款总额6000元,第二次捐款人数比第一次多20人,而且两次人均捐款额正好相等.
|
| |
每桶容积(升) | 20 | 15 |
每桶价格(元) | 5.6 | 4.5 |
(1)求两次各有多少人捐款?
(2)民政部门要求将捐款换成实物,统一运送到灾区.学校决定将捐款用于购买桶装水现有![]() 两种型号桶装水,上表是这两种桶装水的容积和单价.学校按民政局的救灾规划需订购总容积为40000升的桶装水,用同学们的捐款至少需订购
两种型号桶装水,上表是这两种桶装水的容积和单价.学校按民政局的救灾规划需订购总容积为40000升的桶装水,用同学们的捐款至少需订购![]() 型水多少桶.
型水多少桶.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】博文书店举行购书优惠活动:
①一次性购书不超过100元,不享受打折优惠;
②一次性购书超过100元但不超过200元一律打九折;
③一次性购书200元以上一律打七折.
小丽在这次活动中,两次购书总共付款229.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
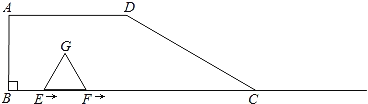
【题目】如图,四边形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°,点E、F同时从B点出发,沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG.设E点移动距离为x(0<x<6).
(1)点G在四边形ABCD的边上时,x= ;点F与点C重合时,x= ;
(2)求出使△DFC成为等腰三角形的x的值;
(3)求△EFG与四边形ABCD重叠部分的面积y与x之间的函数关系式,并直接写出y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠C=90°,点A、B在∠C的两边上,CA=30,CB=20,连结AB.点P从点B出发,以每秒4个单位长度的速度沿BC方向运动,到点C停止.当点P与B、C两点不重合时,作PD⊥BC交AB于D,作DE⊥AC于E.F为射线CB上一点,且∠CEF=∠ABC.设点P的运动时间为x(秒).
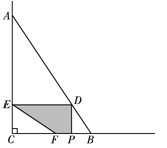
(1)用含有x的代数式表示CE的长;
(2)求点F与点B重合时x的值;
(3)当点F在线段CB上时,设四边形DECP与四边形DEFB重叠部分图形的面积为y(平方单位).求y与x之间的函数关系式;
(4)当x为某个值时,沿PD将以D、E、F、B为顶点的四边形剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合上述条件的x值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com