
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕу![]() ЮЊзјБъдЕуЃЌХзЮяЯп
ЮЊзјБъдЕуЃЌХзЮяЯп![]() НЛ
НЛ![]() жсгк
жсгк![]() СНЕуЃЌНЛ
СНЕуЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() Й§ХзЮяЯпЕФЖЅЕу
Й§ХзЮяЯпЕФЖЅЕу![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌЧв
ЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓ![]() КЭ
КЭ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕу![]() дкЕу
дкЕу![]() КЭЕу
КЭЕу![]() жЎМфЕФХзЮяЯпЩЯЃЌСЌНг
жЎМфЕФХзЮяЯпЩЯЃЌСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсНЛ
жсНЛ![]() гкЕу
гкЕу![]() ЃЌЕу
ЃЌЕу![]() дкжБЯп
дкжБЯп![]() гвВрЕФ
гвВрЕФ![]() жсЩЯЃЌСЌНг
жсЩЯЃЌСЌНг![]() ЃЌЧв
ЃЌЧв![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌбгГЄ
ЃЌбгГЄ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() ЩЯЃЌСЌНг
ЩЯЃЌСЌНг![]() ЃЌШє
ЃЌШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉСю![]() ЃЌЧѓГі
ЃЌЧѓГі![]() ЃЌ
ЃЌ![]() ЃЌЩшХзЮяЯпЖдГЦжсНЛ
ЃЌЩшХзЮяЯпЖдГЦжсНЛ![]() жсгк
жсгк![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЌЧѓГі
ЃЌЧѓГі![]() ЃЌЕУЕН
ЃЌЕУЕН![]() ЃЌДњШы
ЃЌДњШы![]() ЃЌЧѓГіhЃЌЕУЕН
ЃЌЧѓГіhЃЌЕУЕН![]() ЃЌДњШы
ЃЌДњШы![]() ЧѓГіkЃЛ
ЧѓГіkЃЛ
ЃЈ2ЃЉбгГЄ![]() НЛ
НЛ![]() жсгк
жсгк![]() ЃЌЩш
ЃЌЩш![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌИљОне§ЧаЖЈвхПЩЕУ
ЃЌИљОне§ЧаЖЈвхПЩЕУ![]() ЃЌМД
ЃЌМД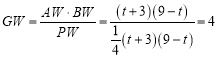 ЃЌгЩ
ЃЌгЩ![]() ЃЌЧѓГі
ЃЌЧѓГі![]() ЃЌДгЖјЧѓГі
ЃЌДгЖјЧѓГі![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЛљБОЫМТЗЃКЙЙдьжБНЧШ§НЧаЮЃЌРћгУе§ЧаЖЈвхСаГіЕШЪНЃЎМДЃКбгГЄ![]() КЭ
КЭ![]() НЛгкЕу
НЛгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌдк
ЃЌдк![]() ЩЯШЁЕу
ЩЯШЁЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЎИљОнЦНааЯпЗжЯпЖЮГЩБШР§ПЩЧѓГі
ЃЎИљОнЦНааЯпЗжЯпЖЮГЩБШР§ПЩЧѓГі![]() ЃЌИљОне§ЧаЖЈвхЕУ
ЃЌИљОне§ЧаЖЈвхЕУ![]() ЃЌМД
ЃЌМД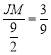 ЃЌЧѓГі
ЃЌЧѓГі![]() ЃЌИљОн
ЃЌИљОн![]() ЃЌЧѓГі
ЃЌЧѓГі![]() ЃЌPNЃЌЕУЕН
ЃЌPNЃЌЕУЕН![]() ЃЌДњШыНтЮіЪНЧѓГіtЃЌдйЕУЕНWEЃЌNTЃЌTKЃЛЩш
ЃЌДњШыНтЮіЪНЧѓГіtЃЌдйЕУЕНWEЃЌNTЃЌTKЃЛЩш![]() ЃЌЧѓГі
ЃЌЧѓГі![]() ЃЌИљОнжБНЧШ§НЧаЮаджЪЕУЕН
ЃЌИљОнжБНЧШ§НЧаЮаджЪЕУЕН![]() ЃЌЙЪ
ЃЌЙЪ![]() ЃЌ
ЃЌ![]() ЃЌМД
ЃЌМД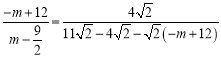 ЃЎ
ЃЎ
НтЃКЃЈ1ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌНтЕУЃЌ
ЃЌНтЕУЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
ЩшХзЮяЯпЖдГЦжсНЛ![]() жсгк
жсгк![]() ЃЌ
ЃЌ
Ёр![]() ЃЌЩш
ЃЌЩш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌДњШы
ЃЌДњШы![]() ЃЌ
ЃЌ
МД![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
Ёр![]() ДњШЫ
ДњШЫ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЃЈ2ЃЉбгГЄ![]() НЛ
НЛ![]() жсгк
жсгк![]() ЃЌ
ЃЌ
Щш![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌЁр
ЃЌЁр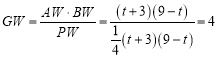 ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌЁр
ЃЌЁр![]() ЃЛ
ЃЛ
ЃЈ3ЃЉбгГЄ![]() КЭ
КЭ![]() НЛгкЕу
НЛгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌдк
ЃЌдк![]() ЩЯШЁЕу
ЩЯШЁЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМД
ЃЌМД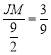 ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌНтЕУЃЌ
ЃЌНтЕУЃЌ![]() Лђ
Лђ![]() ЃЈЩсЃЉЃЌ
ЃЈЩсЃЉЃЌ
Ёр![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
Щш![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ИљОнжБНЧШ§НЧаЮаджЪЕУ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
МД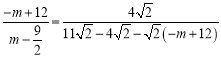 ЃЌ
ЃЌ
НтЕУ![]() Лђ
Лђ![]() ЃЌ
ЃЌ
Ёр![]() Лђ
Лђ![]() ЃЎ
ЃЎ




| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁЖОХеТЫуЪѕЁЗЪЧжаЙњДЋЭГЪ§бЇзюживЊЕФжјзїЃЌдкЁАЙДЙЩЁБеТжагаетбљвЛИіЮЪЬтЃКЁАНёгавиЗНЖўАйВНЃЌИїжаПЊУХЃЌГіЖЋУХЪЎЮхВНгаФОЃЌЮЪЃКГіФЯУХМИВНЖјМћФОЃПЁБ
гУНёЬьЕФЛАЫЕЃЌДѓвтЪЧЃКШчЭМЃЌ![]() ЪЧвЛзљБпГЄЮЊ200ВНЃЈЁАВНЁБЪЧЙХДњЕФГЄЖШЕЅЮЛЃЉЕФе§ЗНаЮаЁГЧЃЌЖЋУХ
ЪЧвЛзљБпГЄЮЊ200ВНЃЈЁАВНЁБЪЧЙХДњЕФГЄЖШЕЅЮЛЃЉЕФе§ЗНаЮаЁГЧЃЌЖЋУХ![]() ЮЛгк
ЮЛгк![]() ЕФжаЕуЃЌФЯУХ
ЕФжаЕуЃЌФЯУХ![]() ЮЛгк
ЮЛгк![]() ЕФжаЕуЃЌГіЖЋУХ15ВНЕФ
ЕФжаЕуЃЌГіЖЋУХ15ВНЕФ![]() ДІгавЛЪїФОЃЌЧѓГіФЯУХЖрЩйВНЧЁКУПДЕНЮЛгк
ДІгавЛЪїФОЃЌЧѓГіФЯУХЖрЩйВНЧЁКУПДЕНЮЛгк![]() ДІЕФЪїФОЃЈМДЕу
ДІЕФЪїФОЃЈМДЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЉЃПЧыФуМЦЫу
ЩЯЃЉЃПЧыФуМЦЫу![]() ЕФГЄЮЊ__________ВНЃЎ
ЕФГЄЮЊ__________ВНЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
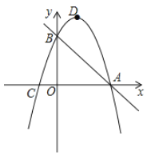
ЁОЬтФПЁПвбжЊЃЌШчЭМЃЌХзЮяЯп![]() ОЙ§жБЯп
ОЙ§жБЯп![]() гызјБъжсЕФСНИіНЛЕу
гызјБъжсЕФСНИіНЛЕу![]() ЃЎДЫХзЮяЯпгы
ЃЎДЫХзЮяЯпгы![]() жсЕФСэвЛИіНЛЕуЮЊ
жсЕФСэвЛИіНЛЕуЮЊ![]() ЃЎХзЮяЯпЕФЖЅЕуЮЊ
ЃЎХзЮяЯпЕФЖЅЕуЮЊ![]() ЃЎ
ЃЎ
![]() ЧѓДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЧѓДЫХзЮяЯпЕФНтЮіЪНЃЛ
![]() ШєЕу
ШєЕу![]() ЮЊХзЮяЯпЩЯвЛЖЏЕуЃЌЪЧЗёДцдкЕу
ЮЊХзЮяЯпЩЯвЛЖЏЕуЃЌЪЧЗёДцдкЕу![]() ЃЎЪЙ
ЃЎЪЙ![]() гы
гы![]() ЕФУцЛ§ЯрЕШ?ШєДцдкЃЌЧѓЕу
ЕФУцЛ§ЯрЕШ?ШєДцдкЃЌЧѓЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшADЮЊЁЯBACЕФЦНЗжЯпЃЌABЃН8ЃЌACЃН10ЃЌADЃН6ЃЌEЮЊACЩЯвЛЕуЃЌAEЃН2ЃЌMЮЊAEЕФжаЕуЃЌNЮЊBCЕФжаЕуЃЌдђMNЃНЃЈЁЁЁЁЃЉ
A.5B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
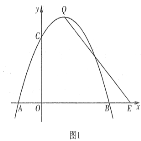
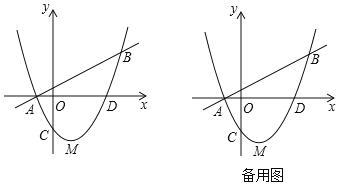
ЁОЬтФПЁПШчЭМвбжЊжБЯп![]() гыХзЮяЯпy=ax2+bx+cЯрНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌmЃЉСНЕуЃЌХзЮяЯпy=ax2+bx+cНЛyжсгкЕуCЃЈ0ЃЌЉ
гыХзЮяЯпy=ax2+bx+cЯрНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌmЃЉСНЕуЃЌХзЮяЯпy=ax2+bx+cНЛyжсгкЕуCЃЈ0ЃЌЉ![]() ЃЉЃЌНЛxжсе§АыжсгкDЕуЃЌХзЮяЯпЕФЖЅЕуЮЊMЃЎ
ЃЉЃЌНЛxжсе§АыжсгкDЕуЃЌХзЮяЯпЕФЖЅЕуЮЊMЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
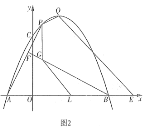
ЃЈ2ЃЉЩшЕуPЮЊжБЯпABЯТЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЌЕБЁїPABЕФУцЛ§зюДѓЪБЃЌЧѓЁїPABЕФУцЛ§МАЕуPЕФзјБъЃЛ
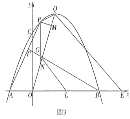
ЃЈ3ЃЉШєЕуQЮЊxжсЩЯвЛЖЏЕуЃЌЕуNдкХзЮяЯпЩЯЧвЮЛгкЦфЖдГЦжсгвВрЃЌЕБЁїQMNгыЁїMADЯрЫЦЪБЃЌЧѓNЕуЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПВЉЮФЪщЕъОйааЙКЪщгХЛнЛюЖЏЃК
ЂйвЛДЮадЙКЪщВЛГЌЙ§100дЊЃЌВЛЯэЪмДђелгХЛнЃЛ
ЂквЛДЮадЙКЪщГЌЙ§100дЊЕЋВЛГЌЙ§200дЊвЛТЩДђОХелЃЛ
ЂлвЛДЮадЙКЪщ200дЊвдЩЯвЛТЩДђЦпелЃЎ
аЁРідкетДЮЛюЖЏжаЃЌСНДЮЙКЪщзмЙВИЖПю229.4дЊЃЌЕкЖўДЮЙКЪщдМлЪЧЕквЛДЮЙКЪщдМлЕФ3БЖЃЌФЧУДаЁРіетСНДЮЙКЪщдМлЕФзмКЭЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
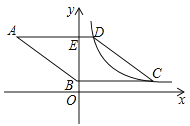
ЁОЬтФПЁПШчЭМЃЌСтаЮ![]() ЕФБп
ЕФБп![]() жсЃЌДЙзуЮЊЕу
жсЃЌДЙзуЮЊЕу![]() ЃЌЖЅЕу
ЃЌЖЅЕу![]() дкЕкЖўЯѓЯоЃЌЖЅЕу
дкЕкЖўЯѓЯоЃЌЖЅЕу![]() дк
дк![]() жсЕФе§АыжсЩЯЃЌЗДБШР§КЏЪ§
жсЕФе§АыжсЩЯЃЌЗДБШР§КЏЪ§![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЕФЭМЯѓЭЌЪБОЙ§ЖЅЕу
ЃЉЕФЭМЯѓЭЌЪБОЙ§ЖЅЕу![]() ЃЌ
ЃЌ![]() ЃЌШєЕу
ЃЌШєЕу![]() ЕФКсзјБъЮЊ10ЃЌ
ЕФКсзјБъЮЊ10ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФжЕЮЊ_______ЃЎ
ЕФжЕЮЊ_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊЕуAЃЌBЃЌCЪЧЁбOЩЯЕФШ§ЕуЃЌвдABЃЌBCЮЊСкБпзїABCDЃЌбгГЄADЃЌНЛЁбOгкЕуEЃЌЙ§ЕуAзїCEЕФЦНааЯпЃЌНЛCDЕФбгГЄЯпгкFЃЎ
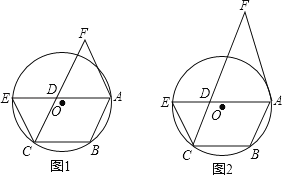
ЃЈ1ЃЉЧѓжЄЃКFDЃНFAЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНгACЃЌШєЁЯFЃН40ЁуЃЌЧвAFЧЁКУЪЧЁбOЕФЧаЯпЃЌЧѓЁЯCABЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁА2017ФъеХбЇгббнГЊЛсЁБгк6дТ3ШедкЮвЪаЙиЩНКўАТЬхжааФОйАьЃЌаЁеХШЅРыМв2520УзЕФАТЬхжааФПДбнГЊЛсЃЌЕНАТЬхжааФКѓЃЌЗЂЯжбнГЊЛсУХЦБЭќДјСЫЃЌДЫЪБРыбнГЊЛсПЊЪМЛЙга23ЗжжгЃЌгкЪЧЫћХмВНЛиМвЃЌФУЕНЦБКѓСЂПЬевЕНвЛСОЁАЙВЯэЕЅГЕЁБдТЗИЯЛиАТЬхжааФЃЌвбжЊаЁеХЦяГЕЕФЪБМфБШХмВНЕФЪБМфЩйгУСЫ4ЗжжгЃЌЧвЦяГЕЕФЦНОљЫйЖШЪЧХмВНЕФЦНОљЫйЖШЕФ1.5БЖЃЎ
ЃЈ1ЃЉЧѓаЁеХХмВНЕФЦНОљЫйЖШЃЛ
ЃЈ2ЃЉШчЙћаЁеХдкМвШЁЦБКЭбАевЁАЙВЯэЕЅГЕЁБЙВгУСЫ5ЗжжгЃЌЫћФмЗёдкбнГЊЛсПЊЪМЧАИЯЕНАТЬхжааФЃПЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com