
【题目】如图1,已知点A,B,C是⊙O上的三点,以AB,BC为邻边作ABCD,延长AD,交⊙O于点E,过点A作CE的平行线,交CD的延长线于F.
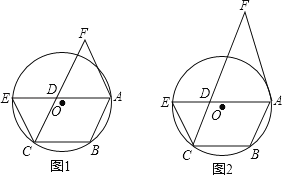
(1)求证:FD=FA;
(2)如图2,连接AC,若∠F=40°,且AF恰好是⊙O的切线,求∠CAB的度数.
【答案】(1)见解析;(2)∠CAB=30°.
【解析】
(1)连接CA,如图1,先证明∠1=∠2得到弧CE=弧AB,则弧EB=弧AC,所以∠BAE=∠E,然后证明∠3=∠4得到FA=FD;
(2)连接OA、OC,如图2,利用三角形内角和计算出∠FAD=∠FDA=70°,再根据平行线的性质得到∠E=∠FAD=70°,∠BAD=∠FDA=70°,接着根据圆周角定理得到∠AOC=2∠E=140°,利用等腰三角形的性质得到∠OAC=20°,然后利用切线的性质得到∠OAF=90°,于是计算∠BAF-∠OAF-∠OAC即可.
(1)证明:连接CA,如图1,
∵四边形ABCD为平行四边形,
∴AE//BC,AB//CF,
∴∠1=∠2,
∴弧CE=弧AB,
∴弧CE+弧BC=弧AB+弧BC,即弧EB=弧AC,
∴∠BAE=∠E,
∵AB//CF,
∴∠4=∠BAE,
∵AF//CE,
∴∠E=∠3,
∴∠3=∠4,
∴FA=FD;
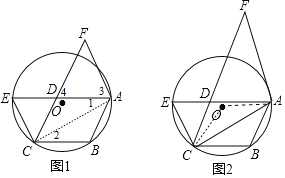
(2)解:连接OA、OC,如图2,
∵∠F=40°,
∴∠FAD=∠FDA=70°,
∴∠E=∠FAD=70°,∠BAD=∠FDA=70°,
∵∠AOC=2∠E=140°,∠BAF=∠FAD+∠BAD =140°,
而OC=OA,
∴∠OAC=![]() (180°﹣140°)=20°,
(180°﹣140°)=20°,
∵AF为切线,
∴OA⊥AF,
∴∠OAF=90°,
∴∠CAB=∠BAF﹣∠OAF﹣∠OAC=140°﹣90°﹣20°=30°.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等的凸四边形叫做“准菱形”.利用该定义完成以下各题:
(1) 理解
填空:如图1,在四边形ABCD中,若 (填一种情况),则四边形ABCD是“准菱形”;
(2)应用
证明:对角线相等且互相平分的“准菱形”是正方形;(请画出图形,写出已知,求证并证明)
(3) 拓展
如图2,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BP方向平移得到△DEF,连接AD,BF,若平移后的四边形ABFD是“准菱形”,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
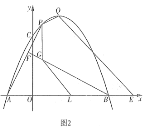
【题目】如图1,在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 过抛物线的顶点
过抛物线的顶点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
(2)如图2,点![]() 在点
在点![]() 和点
和点![]() 之间的抛物线上,连接
之间的抛物线上,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 右侧的
右侧的![]() 轴上,连接
轴上,连接![]() ,且
,且![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)如图3,在(2)的条件下,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
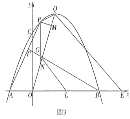
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求这个二次函数的解析式;
(2)点![]() 是直线
是直线![]() 上方的抛物线上一动点,是否存在点
上方的抛物线上一动点,是否存在点![]() ,使得
,使得![]() 的面积最大?若存在,求出点
的面积最大?若存在,求出点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(3)点![]() 是直线
是直线![]() 上方的抛物线上一动点,过点
上方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() .是否存在点
.是否存在点![]() ,使以点
,使以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,直接写出点
相似?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正六边形ABCDEF的边长为![]() ,点G,H,I,J,K,L依次在正六边形的六条边上,且AG=BH=CI=DJ=EK=FL,顺次连结G,I,K,和H,J,L,则图中阴影部分的周长C的取值范围为( )
,点G,H,I,J,K,L依次在正六边形的六条边上,且AG=BH=CI=DJ=EK=FL,顺次连结G,I,K,和H,J,L,则图中阴影部分的周长C的取值范围为( )
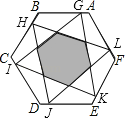
A.6≤C≤6![]() B.3≤C≤3
B.3≤C≤3![]() C.3
C.3![]() ≤C≤6D.3
≤C≤6D.3![]() ≤C≤6
≤C≤6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南宁海吉星水果批发市场李大姐家的水果店销售三华李,根据前段时间的销售经验,每天的售价![]() (元/箱)与销售量
(元/箱)与销售量![]() (箱)有如表关系,且已知
(箱)有如表关系,且已知 ![]() 与 x 之间的函数关系是一次函数.
与 x 之间的函数关系是一次函数.
每箱售价x(元) | 68 | 67 | 66 | 65 | … | 40 |
每天销量y(箱) | 40 | 45 | 50 | 55 | … | 180 |
(1)求y 与x的函数解析式;
(2)三华李的进价是 40 元/箱,如果设每天获得的盈利为 ![]() 元,要使该店每天获得最大盈利,则每箱售价多少元?
元,要使该店每天获得最大盈利,则每箱售价多少元?
(3)4 月份(按 30 天算)连续阴雨,销售量减少.该店决定采取降价销售,故在(2)的条件下销售了 18 天之后,三华李开始降价,售价比之前下降了![]() ,同时三华李的进价降为 29 元/箱,销售量也因此比原来每天获得最大盈利时上涨了
,同时三华李的进价降为 29 元/箱,销售量也因此比原来每天获得最大盈利时上涨了![]() ,降价销售了 12 天的三华李销售总盈利比降价销售前的销售总盈利少 5670 元,求
,降价销售了 12 天的三华李销售总盈利比降价销售前的销售总盈利少 5670 元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张同学学完统计知识后,随机调查了她所在辖区若干名居民的年龄,将调查数据绘制成如下扇形统计图和条形统计图:


请根据以上不完整的统计图提供的信息,解答下列问题:
(1)小张同学共调查了_____名居民的年龄,扇形统计图中a=_____;
(2)补全条形统计图,并注明人数;
(3)若在该辖区中随机抽取一人,那么这个人年龄是60岁及以上的概率为_____;
(4)若该辖区年龄在0~14岁的居民约有3500人,请估计该辖区居民人数是_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
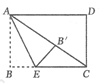
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,把
,把![]() 沿
沿![]() 折叠,点
折叠,点![]() 落点为
落点为![]() ,当
,当![]() 为直角三角形时,
为直角三角形时,![]() 的长为__________;在折叠过程中,
的长为__________;在折叠过程中,![]() 的最小值为__________.
的最小值为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com