
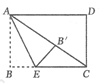
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,把
,把![]() 沿
沿![]() 折叠,点
折叠,点![]() 落点为
落点为![]() ,当
,当![]() 为直角三角形时,
为直角三角形时,![]() 的长为__________;在折叠过程中,
的长为__________;在折叠过程中,![]() 的最小值为__________.
的最小值为__________.
【答案】![]() 或3 1
或3 1
【解析】
(1)先根据直角三角形的定义分两种情况:![]() 和
和![]() ,再根据折叠的性质、矩形的判定与性质分别得出点
,再根据折叠的性质、矩形的判定与性质分别得出点![]() 的位置,然后分别根据折叠的性质、勾股定理、矩形的性质求解即可得BE的长;
的位置,然后分别根据折叠的性质、勾股定理、矩形的性质求解即可得BE的长;
(2)利用折叠的性质、三角形的三边关系定理即可得.
(1)由直角三角形的定义,分以下两种情况:
①当![]() 时,
时,![]() 为直角三角形
为直角三角形
如图1,连接AC
![]() 四边形ABCD是矩形,
四边形ABCD是矩形,![]() ,
,![]()
![]() ,
,![]()
由折叠的性质可知,![]()
![]()
![]() 点
点![]() 共线,即
共线,即![]() 沿AE折叠时,点B的对应点
沿AE折叠时,点B的对应点![]() 落在对角线AC上
落在对角线AC上
![]()
设![]() ,则
,则![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]() ,即
,即![]()

②当![]() 时,
时,![]() 为直角三角形
为直角三角形
![]()
![]() 四边形ABCD是矩形,
四边形ABCD是矩形,![]() ,
,![]()
![]() ,
,![]()
由折叠的性质可知,![]()
![]() 四边形
四边形![]() 和四边形
和四边形![]() 均为矩形
均为矩形
![]() ,
,![]()
![]()
![]() 点
点![]() 共线,即
共线,即![]() 沿AE折叠时,点B的对应点
沿AE折叠时,点B的对应点![]() 落在边AD上
落在边AD上
则![]()
综上,BE的长为![]() 或3
或3
故答案为:![]() 或3;
或3;
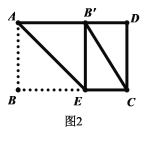
(2)由折叠和矩形的性质得:![]() ,
,![]()
如图3-1,在折叠过程中,当点![]() 不落在边AD上时,点
不落在边AD上时,点![]() 总能构成一个三角形,即
总能构成一个三角形,即![]()
由三角形的三边关系定理得:![]()
如图3-2,在折叠过程中,当点![]() 恰好落在边AD上时,点
恰好落在边AD上时,点![]() 共线
共线
此时,![]()
综上,![]() 的取值范围为
的取值范围为![]()
则![]() 的最小值为1
的最小值为1
故答案为:1.



科目:初中数学 来源: 题型:
【题目】如图1,已知点A,B,C是⊙O上的三点,以AB,BC为邻边作ABCD,延长AD,交⊙O于点E,过点A作CE的平行线,交CD的延长线于F.
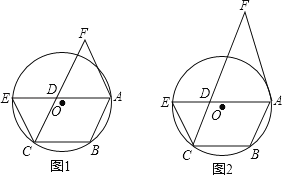
(1)求证:FD=FA;
(2)如图2,连接AC,若∠F=40°,且AF恰好是⊙O的切线,求∠CAB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2017年张学友演唱会”于6月3日在我市关山湖奥体中心举办,小张去离家2520米的奥体中心看演唱会,到奥体中心后,发现演唱会门票忘带了,此时离演唱会开始还有23分钟,于是他跑步回家,拿到票后立刻找到一辆“共享单车”原路赶回奥体中心,已知小张骑车的时间比跑步的时间少用了4分钟,且骑车的平均速度是跑步的平均速度的1.5倍.
(1)求小张跑步的平均速度;
(2)如果小张在家取票和寻找“共享单车”共用了5分钟,他能否在演唱会开始前赶到奥体中心?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
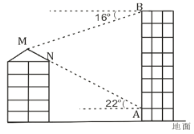
【题目】如图,小明在商城二楼地板![]() 处发现对五层居民楼顶防雨棚一侧斜面
处发现对五层居民楼顶防雨棚一侧斜面![]() 与点
与点![]() 在一条直线上,此时测得
在一条直线上,此时测得![]() ,
,![]() 仰角是
仰角是![]() ,上到九楼在地板边沿
,上到九楼在地板边沿![]() 点测得居民楼顶斜面顶端
点测得居民楼顶斜面顶端![]() 点俯角是
点俯角是![]() ,已知商城每层楼高
,已知商城每层楼高![]() 米,居民楼每层楼高
米,居民楼每层楼高![]() 米,试计算居民楼顶防雨棚一侧斜面
米,试计算居民楼顶防雨棚一侧斜面![]() 的长度.(结果保留精确到
的长度.(结果保留精确到![]() 米)(参考数据:
米)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
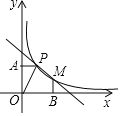
【题目】如图,已知反比例函数![]() 的图象和一次函数
的图象和一次函数![]() 的图象都过点
的图象都过点![]() ,过点P作y轴的垂线,垂足为A,O为坐标原点,
,过点P作y轴的垂线,垂足为A,O为坐标原点,![]() 的面积为1.
的面积为1.
(1)求反比例函数和一次函数的解析式;
(2)设反比例函数图象与一次函数图象的另一交点为M,过M作x轴的垂线,垂足为B,求五边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
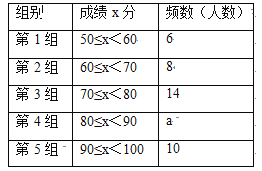
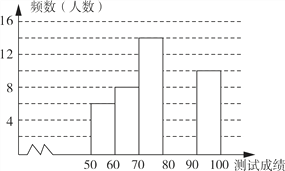
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表.
请结合图表完成下列各题:
(1)① 表中a的值为 ;
② 把频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长均为1,有线段![]() 和线段
和线段![]() ,点
,点![]() 、
、![]() 、
、![]() 、
、![]() 均在小正方形的顶点上.
均在小正方形的顶点上.
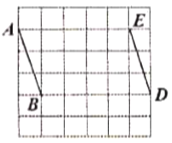
(1)在图中画出以![]() 为斜边的直角三角形
为斜边的直角三角形![]() ,点
,点![]() 在小正方形的顶点上,且直角三角形
在小正方形的顶点上,且直角三角形![]() 的面积为5;
的面积为5;
(2)在图中画出以![]() 为一边的正方形
为一边的正方形![]() 点
点![]() 在小正方形的顶点上,并直接写出直角三角形
在小正方形的顶点上,并直接写出直角三角形![]() 与正方形
与正方形![]() 重叠部分的面积.
重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的对角线AC、BD相交于点O,过O点作OE⊥AC,交AB于E,若BC=4,△AOE的面积是5,则下列说法错误的是( )
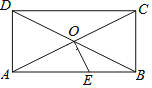
A.AE=5B.∠BOE=∠BCEC.CE⊥OBD.sin∠BOE=0.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com