
【题目】如图,已知矩形ABCD的对角线AC、BD相交于点O,过O点作OE⊥AC,交AB于E,若BC=4,△AOE的面积是5,则下列说法错误的是( )
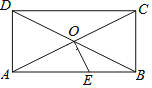
A.AE=5B.∠BOE=∠BCEC.CE⊥OBD.sin∠BOE=0.6
【答案】C
【解析】
过点O作OF⊥AD于F,作OG⊥AB于G,构建矩形AGOF,求出OG的长,利用三角形的面积公式可求得AE的长,进而可判断选项A;通过证明E、B、C、O四点共圆,进而可判断选项B;由E、B、C、O四点共圆,根据垂径定理可知,要想OB⊥CE,通过判断弦长BE和OE的大小即可,进而可判断选项C;利用同角的三角函数计算,进而可判断选项D.
A、过O作OF⊥AD于F,作OG⊥AB于G,
∵四边形ABCD是矩形,
∴AC=BD,OA=![]() AC,OD=
AC,OD=![]() BD,
BD,
∴OA=OD,
∴AF=FD=![]() AD=
AD=![]() BC=2,
BC=2,
∵∠AGO=∠BAD=∠AFO=90°,
∴四边形AGOF是矩形,
∴OG=AF=2,
∵S△AEO=![]() AEOG=5,
AEOG=5,
∴AE=5,
所以此选项的说法正确;
B、连接CE,∵OE⊥AC,
∴∠EOC=90°
∵∠ABC=90°,
∴∠ABC+∠EOC=180°,
∴E、B、C、O四点共圆,
∴∠BCE=∠BOE,
所以此选项的说法正确;
C、在Rt△BEC中,由勾股定理得:BE=![]() ,
,
∴AB=3+5=8,
∴AC=![]() ,
,
∴AO=![]() AC=
AC=![]() ,
,
∴EO=![]() ,
,
∴OE≠BE,
∵E、B、C、O四点共圆,
∵∠EOC=90°,
∴EC是直径,
∴EC与OB不垂直;
此选项的说法不正确;
D、sin∠BOE=sin∠BCE=![]() ,
,
所以此选项的说法正确,
因为本题选择说法错误的,
故选C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
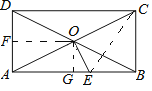
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,把
,把![]() 沿
沿![]() 折叠,点
折叠,点![]() 落点为
落点为![]() ,当
,当![]() 为直角三角形时,
为直角三角形时,![]() 的长为__________;在折叠过程中,
的长为__________;在折叠过程中,![]() 的最小值为__________.
的最小值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
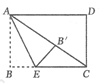
【题目】如图,在平面直角坐标系xOy中,一次函数y=x与二次函数![]() 的图象相交于O、A两点,点A(3,3),点M为抛物线的顶点.
的图象相交于O、A两点,点A(3,3),点M为抛物线的顶点.
(1)求二次函数的表达式;
(2)长度为![]() 的线段PQ在线段OA(不包括端点)上滑动,分别过点P、Q作x轴的垂线交抛物线于点P1、Q1,求四边形PQQ1P1面积的最大值;
的线段PQ在线段OA(不包括端点)上滑动,分别过点P、Q作x轴的垂线交抛物线于点P1、Q1,求四边形PQQ1P1面积的最大值;
(3)直线OA上是否存在点E,使得点E关于直线MA的对称点F满足S△AOF=S△AOM?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长六寸,问径几何?”用现代的数学语言表述是:“CD为![]() 的直径,弦
的直径,弦![]() ,垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意得CD的长为( )
,垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意得CD的长为( )
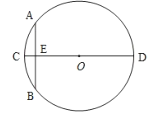
A.12寸B.13寸C.24寸D.26寸
查看答案和解析>>
科目:初中数学 来源: 题型:
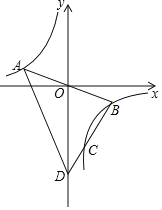
【题目】如图,反比例函数y=![]() (k≠0)的图象经过△ABD的顶点A,B,交BD于点C,AB经过原点,点D在y轴上,若BD=4CD,△OBD的面积为15,则k的值为_____.
(k≠0)的图象经过△ABD的顶点A,B,交BD于点C,AB经过原点,点D在y轴上,若BD=4CD,△OBD的面积为15,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
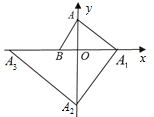
【题目】如图,在平面直角坐标系中点A(0,3),![]() ,过点A作AB的垂线交x轴于点A1,过A1作AA1的垂线交y轴于点A2,过点A2作A1A2的垂线交x轴于点A3……,按此规律继续作下去,直至得到点A2018为止,则点A2018坐标为__________.
,过点A作AB的垂线交x轴于点A1,过A1作AA1的垂线交y轴于点A2,过点A2作A1A2的垂线交x轴于点A3……,按此规律继续作下去,直至得到点A2018为止,则点A2018坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
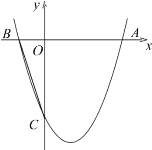
【题目】如图,二次函数![]() 的图像与x轴交于A,B两点(点B在点A左侧),与y轴负半轴相交于点C,且tan∠ABC=3,
的图像与x轴交于A,B两点(点B在点A左侧),与y轴负半轴相交于点C,且tan∠ABC=3,
(1)求该二次函数的解析式;
(2)设E是位于第四象限抛物线上的一个动点,过E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH,则在点E运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
(3)设点P是x轴下方的抛物线上的一个动点,连接PA、PC,求△PAC面积的取值范围,当△PAC面积为整数时,这样的△PAC有几个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市中招体育测试改革,其中篮球和足球作为选考项目,某商店抓住这一商机决定购进一批篮球和足球共200个,这两种球的进价和售价如下表所示:
篮球 | 足球 | |
进价(元/个) | 180 | 150 |
售价(元/个) | 250 | 200 |
(1)若商店计划销售完这批球后能获利11600元,问篮球和足球应分别购进多少个?
(2)设购进篮球![]() 个,获利为
个,获利为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系;
之间的函数关系;
(3)若商店计划投入资金不多于31560元且销售完这批球后商店获利不少于11000元,请问有哪几种购球方案,并写出获利最大的购球方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
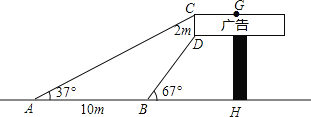
【题目】数学兴趣小组想利用所学的知识了解某广告牌的高度,已知CD=2m.经测量,得到其它数据如图所示.其中∠CAH=37°,∠DBH=67°,AB=10m,请你根据以上数据计算GH的长.(参考数据![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com