
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
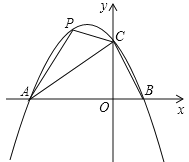
(1)求这个二次函数的解析式;
(2)点![]() 是直线
是直线![]() 上方的抛物线上一动点,是否存在点
上方的抛物线上一动点,是否存在点![]() ,使得
,使得![]() 的面积最大?若存在,求出点
的面积最大?若存在,求出点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(3)点![]() 是直线
是直线![]() 上方的抛物线上一动点,过点
上方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() .是否存在点
.是否存在点![]() ,使以点
,使以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,直接写出点
相似?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)存在,点
;(2)存在,点![]() ;(3)存在,
;(3)存在,![]() ,
,![]() .
.
【解析】
(1)把点A、B的坐标代入二次函数解析式,利用待定系数法求二次函数解析式解答;
(2)连接![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,得出
,得出![]() ,从而推出
,从而推出![]() ,即可推出当
,即可推出当![]() 时,
时,![]() 的面积最大,从而求出点
的面积最大,从而求出点![]() 的坐标.
的坐标.
(3)设点E的横坐标为c,表示出BE、QE,然后根据相似三角形对应边成比例,分OA和BE,OA和QE是对应边两种情况列出比例式求解即可.
(1)由抛物线![]() 过点
过点![]() ,
,![]() ,
,
则![]() ,解得
,解得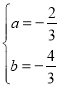 .
.
![]() 二次函数的解析式为
二次函数的解析式为![]() .
.
(2)存在.如图,连接![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() .
.
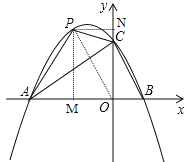
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() .
.
![]() ,
,![]() ,
,![]() .
.
![]() 当
当![]() 时,
时,![]() ,
,
![]() .
.
![]()
![]()
![]()
![]() .
.
![]() ,
,
![]() 当
当![]() 时,
时,![]() 有最大值.
有最大值.
此时![]() .
.
![]() 存在点
存在点![]() ,使
,使![]() 的面积最大.
的面积最大.
(3)存在点![]() ,坐标为
,坐标为![]() ,
,![]() .
.
理由如下:设点E的横坐标为c,则点Q的坐标为![]() BE=1-c,
BE=1-c,
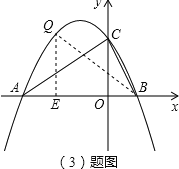
①OA和BE是对应边时,∵△BEQ∽△AOC,
∴![]() ,
,
即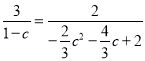 ,
,
整理得,c2+c-2=0,
解得c1=-2,c2=1(舍去),
此时,![]() ,
,
点Q(-2,2);
②OA和QE是对应边时,∵△QEB∽△AOC,
∴![]() ,
,
即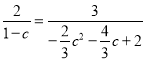 ,
,
整理得,4c2-c-3=0,
解得![]() ,c2=1(舍去),
,c2=1(舍去),
此时,![]() ,
,
点![]() ;
;
综上所述,存在点![]() ,
,![]() 使以点B、Q、E为顶点的三角形与△AOC相似.
使以点B、Q、E为顶点的三角形与△AOC相似.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】设AD为∠BAC的平分线,AB=8,AC=10,AD=6,E为AC上一点,AE=2,M为AE的中点,N为BC的中点,则MN=( )
A.5B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】博文书店举行购书优惠活动:
①一次性购书不超过100元,不享受打折优惠;
②一次性购书超过100元但不超过200元一律打九折;
③一次性购书200元以上一律打七折.
小丽在这次活动中,两次购书总共付款229.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形![]() 的边
的边![]() 轴,垂足为点
轴,垂足为点![]() ,顶点
,顶点![]() 在第二象限,顶点
在第二象限,顶点![]() 在
在![]() 轴的正半轴上,反比例函数
轴的正半轴上,反比例函数![]() (
(![]() ,
,![]() )的图象同时经过顶点
)的图象同时经过顶点![]() ,
,![]() ,若点
,若点![]() 的横坐标为10,
的横坐标为10,![]() ,则
,则![]() 的值为_______.
的值为_______.
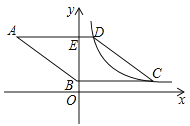
查看答案和解析>>
科目:初中数学 来源: 题型:
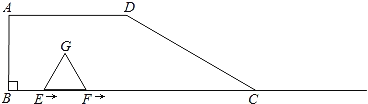
【题目】如图,四边形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°,点E、F同时从B点出发,沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG.设E点移动距离为x(0<x<6).
(1)点G在四边形ABCD的边上时,x= ;点F与点C重合时,x= ;
(2)求出使△DFC成为等腰三角形的x的值;
(3)求△EFG与四边形ABCD重叠部分的面积y与x之间的函数关系式,并直接写出y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点A,B,C是⊙O上的三点,以AB,BC为邻边作ABCD,延长AD,交⊙O于点E,过点A作CE的平行线,交CD的延长线于F.
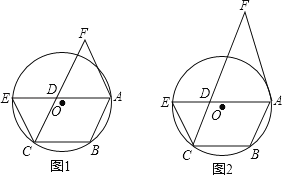
(1)求证:FD=FA;
(2)如图2,连接AC,若∠F=40°,且AF恰好是⊙O的切线,求∠CAB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是边长为1的正方形ABCD的对角线,BE平分∠DBC交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G.
(1)求证:△BCE≌△DCF;
(2)求CF的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
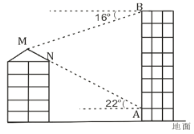
【题目】如图,小明在商城二楼地板![]() 处发现对五层居民楼顶防雨棚一侧斜面
处发现对五层居民楼顶防雨棚一侧斜面![]() 与点
与点![]() 在一条直线上,此时测得
在一条直线上,此时测得![]() ,
,![]() 仰角是
仰角是![]() ,上到九楼在地板边沿
,上到九楼在地板边沿![]() 点测得居民楼顶斜面顶端
点测得居民楼顶斜面顶端![]() 点俯角是
点俯角是![]() ,已知商城每层楼高
,已知商城每层楼高![]() 米,居民楼每层楼高
米,居民楼每层楼高![]() 米,试计算居民楼顶防雨棚一侧斜面
米,试计算居民楼顶防雨棚一侧斜面![]() 的长度.(结果保留精确到
的长度.(结果保留精确到![]() 米)(参考数据:
米)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com