
【题目】如图所示,∠MON=45°,点P是∠MON内一点,过点P作PA⊥OM于点A、PB⊥ON于点B,且PB=2 ![]() .取OP的中点C,联结AC并延长,交OB于点D.
.取OP的中点C,联结AC并延长,交OB于点D.
(1)求证:∠ADB=∠OPB;
(2)设PA=x,OD=y,求y关于x的函数解析式;
(3)分别联结AB、BC,当△ABD与△CPB相似时,求PA的长.
【答案】
(1)
证明:如图,∵PA⊥OM,CO=CP,
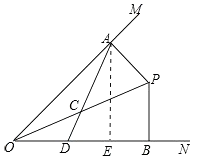
∴CO=CP=CA,
∴∠CAO=∠COA,
过A作AE⊥OB于E,
∵∠MON=45°,
∴∠AOE=∠OAE=45°,
∴∠POB=∠DAE,
∵PB⊥OB,
∴∠ADB=∠OPB
(2)
解:如图1,
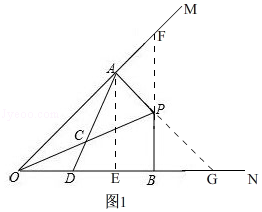
延长BP交OM于F,
∵BP⊥ON,PA⊥OM,
∴∠OBP=∠OAP=90°,
∵∠MON=45°,
∴∠AFB=45°,
在Rt△APF中,AP=x,∠OFB=45°,
∴PF= ![]() x,
x,
∴BF=PF+PB= ![]() x+2
x+2 ![]() =
= ![]() (x+2),
(x+2),
在Rt△OBF中,OB=BF= ![]() (x+2)
(x+2)
延长AP交ON于G,
同理:PG= ![]() PB=4,
PB=4,
∴OA=AG=AP+PG=x+4,
过点A作AE⊥ON,
∴OE=AE= ![]() OA=
OA= ![]() (x+4),
(x+4),
∴DE=OE﹣OD= ![]() (x+4)﹣y
(x+4)﹣y
由(1)知,∠ADE=∠OPB,
∵∠AED=∠OBP=90°,
∴△ADE∽△OPB,
∴ ![]() ,
,
∴ ![]() ,
,
∴y= ![]()
(3)
解:如图2,
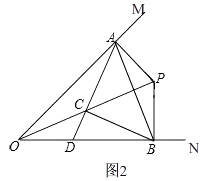
在Rt△OAP中,点C是OP中点,
∴AC=OC= ![]() OP,
OP,
在Rt△OBP中,点C是OP中点,
∴BC=OC= ![]() OP,
OP,
∴AC=BC,
∵AC=OC,
∴∠ACP=2∠AOP,
∵OC=BC,
∴∠BCP=2∠BOP,
∴∠ACB=∠ACP+∠BCP=2(∠AOP+∠BOP)=2∠AOB=90°,
∴∠BAC=∠CAB=45°,
∵∠OBP=90°,
∴∠OBC+∠ABP=45°
∵当△ABD与△CPB相似时,
∵∠ADB=∠CPB,
∴∠ABD=∠PBC,
∴∠OBC=∠ABP= ![]() ×45°=22.5°,
×45°=22.5°,
∵OC=BC,
∴∠BOC=∠OBC=22.5°,
∴∠AOP=∠BOP,
∴OP是∠MON的角平分线,
∵PA⊥OM,PB⊥ON,
∴PA=PB=2 ![]()
【解析】(1)先判断出∠DAE=∠POB,再利用等角的余角相等即可得出结论;(2)先利用等腰直角三角形的性质得出OB=BF= ![]() (x+2),同理得出OA=x+4,即可得出AE,OE,进而得出DE,最后用△ADE∽△OPB的比例式建立方程化简即可得出结论;(3)先利用直角三角形斜边的中线等于斜边的一半和三角形外角的性质判断出△ABC是等腰直角三角形,即可得出∠OBC+∠ABP=45°,再用△ABD与△CPB得出,∠ABD=∠PBC,即∠OBC=∠ABP=
(x+2),同理得出OA=x+4,即可得出AE,OE,进而得出DE,最后用△ADE∽△OPB的比例式建立方程化简即可得出结论;(3)先利用直角三角形斜边的中线等于斜边的一半和三角形外角的性质判断出△ABC是等腰直角三角形,即可得出∠OBC+∠ABP=45°,再用△ABD与△CPB得出,∠ABD=∠PBC,即∠OBC=∠ABP= ![]() ×45°=22.5°,进而得出OP是∠MON的平分线即可得出结论.
×45°=22.5°,进而得出OP是∠MON的平分线即可得出结论.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°,以及对直角三角形斜边上的中线的理解,了解直角三角形斜边上的中线等于斜边的一半.


科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中有一个黑球a和两个白球b,c(除颜色外其他均相同).用树状图(或列表法)解答下列问题:
(1)小丽第一次从袋子中摸出一个球不放回,第二次又从袋子中摸出一个球.则小丽两次都摸到白球的概率是多少?
(2)小强第一次从袋子中摸出一个球,摸到黑球不放回,摸到白球放回;第二次又从袋子中摸出一个球,则小强两次都摸到白球的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是射线BE上一点,过A作CA⊥BE交射线BF于点C,AD⊥BF交射线BF于点D,给出下列结论:①∠1是∠B的余角;②图中互余的角共有3对;③∠1的补角只有∠ACF;④与∠ADB互补的角共有3个.则上述结论正确的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的边长为a.直线y=bx+c交x轴于E,交y轴于F,且a,b,c分别满足:-(a-4)2≥0,c=![]() +
+![]() +8.
+8.
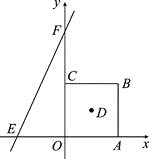
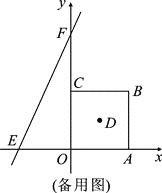
(1)直线y=bx+c的解析式为________;正方形OABC的对角线的交点D的坐标为________;
(2)若正方形OABC沿x轴负方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;
(3)点P为正方形OABC的对角线AC上的动点(端点A、C除外),PM⊥PO,交直线AB于M,在备用图中画图分析,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点A在射线CE上,∠C=∠D.
(1)如图1,若AC∥BD,求证:AD∥BC;
(2)如图2,若∠BAC=∠BAD,BD⊥BC,请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
(3)如图3,在(2)的条件下,过点D作DF∥BC交射线于点F,当∠DFE=8∠DAE时,求∠BAD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于受到手机更新换代的影响,某店经销的甲型号手机今年的售价比去年每台降价500元.如果卖出相同数量的手机,那么去年销售额为8万元,今年销售额只有6万元.
(1)今年甲型号手机每台售价为多少元?
(2)为了提高利润,该店计划购进乙型号手机销售,已知甲型号手机每台进价为1000元,乙型号手机每台进价为800元,预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20台,请问有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年是第39个植树节,我们提出了“追求绿色时尚,走向绿色文明”的倡议.某校为积极响应这一倡议,立即在八、九年级开展征文活动,校团委对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图. 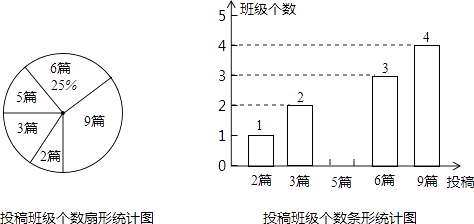
(1)求扇形统计图中投稿3篇的班级个数所对应的扇形的圆心角的度数.
(2)求该校八、九年级各班在这一周内投稿的平均篇数,并将该条形统计图补充完整.
(3)在投稿篇数最多的4个班中,八、九年级各有两个班,校团委准备从这四个班中选出两个班参加全校的表彰会,请你用列表法或画树状图的方法求出所选两个班正好不在同一年级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com