
【题目】如图,在平面直角坐标系中,正方形OABC的边长为a.直线y=bx+c交x轴于E,交y轴于F,且a,b,c分别满足:-(a-4)2≥0,c=![]() +
+![]() +8.
+8.
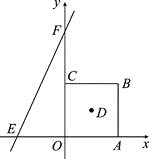
(1)直线y=bx+c的解析式为________;正方形OABC的对角线的交点D的坐标为________;
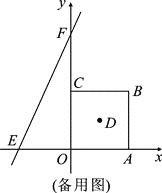
(2)若正方形OABC沿x轴负方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;
(3)点P为正方形OABC的对角线AC上的动点(端点A、C除外),PM⊥PO,交直线AB于M,在备用图中画图分析,直接写出![]() 的值.
的值.
【答案】(1)y=2x+8, D(2,2);(2)t=5;(3)![]() .
.
【解析】
(1)由已知条件易得:a=4,b=2,c=8,由此即可得到直线EF的解析式为:y=2x+8,点B的坐标为(4,4),结合点D是正方形OABC对角线的交点可得点D的坐标为(2,2);
(2)由点D是正方形OABC的对称中心可知,当点D落在直线EF上时,直线EF平分正方形OABC的面积,由已知条件设当点D落在EF上时的坐标为(2-t,2),将此坐标代入直线EF的解析式即可求得对应的t的值;
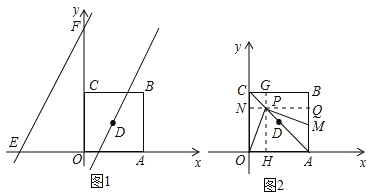
(3)如图2,过P点作PQ∥OA,PH∥CO,交CO、AB于N、Q,交CB、OA于G、H,结合已知条件易证四边形PNCG是正方形,四边形PGBQ是矩形,四边形OHGC是矩形,PH=PQ,∠OPH=∠MPQ,由此证得△OPH≌△MPQ,从而可得QM=OH=CG=GP=BQ=![]() BM,结合PC=
BM,结合PC=![]() GP即可得到PC=
GP即可得到PC=![]() BM,由此即可得到
BM,由此即可得到![]() .
.
(1)∵![]() ,
,
∴![]() 且
且![]() ,
,
∴b=2,c=8,
∴直线y=bx+c的解析式为:y=2x+8;
∵![]() ,
,
∴![]() ,
,
∴a=4,
∴OA=AB=4,
∴点B的坐标为(4,4),
∴点D是正方形OABC对角线的交点,
∴点D是线段OB的交点,
∴点D的坐标为(2,2);
(2)存在,理由如下:
如图1,∵点D是正方形OABC的对角线的交点,
∴过点D的直线都能把正方形AOCB的面积分成相等的两部分,
∴当正方形AOCB平移到直线EF过D点时,直线正好平分正方形的面积,
设平移后的D点坐标为(2-t,2),
把它代入直线y=2x+8,2(2-t)+8=2,
解得:t=5;
(3)如图2,过P点作PQ∥OA,PH∥CO,交CO、AB于N、Q,交CB、OA于G、H,
∵∠OPM=∠HPQ=90°,
∴∠OPH+∠HPM=90°,∠HPM+∠MPQ=90°,
∴∠OPH=∠MPQ,
∵AC为∠BAO平分线,且PH⊥OA,PQ⊥AB,
∴PH=PQ,
在△OPH和△MPQ中: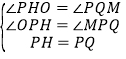
∴△OPH≌△MPQ(AAS),
∴OH=QM,
∵PQ∥OA,PH∥CO,交CO、AB于N、Q,交CB、OA于G、H,四边形AOBC是正方形,
∴易得四边形CNPG为正方形,四边形PGBQ是矩形,四边形OHGC是矩形,
∴PG=BQ=CG=OH=QM,
∴PG=![]() BM,
BM,
∵在正方形CNPG中,PC=![]() PG,
PG,
∴PC=![]() BM,
BM,
∴![]() .
.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:初中数学 来源: 题型:
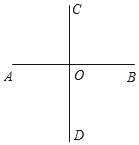
【题目】操作:如图,直线AB与CD交于点O,按要求完成下列问题.
(1)用量角器量得∠AOC= 度.AB与CD的关系可记作 .
(2)画出∠BOC的角平分线OM,∠BOM=∠ = 度.
(3)在射线OM上取一点P,画出点P到直线AB的距离PE.
(4)如图若按“上北下南左西右东”的方位标记,请画出表示“南偏西30°”的射线OF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF. 
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
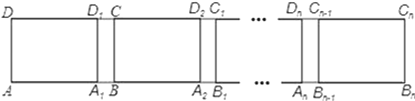
【题目】如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位,得到长方形A1B1C1D1,第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位,得到长方形A2B2C2D2…,第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向平移5个单位,得到长方形AnBnCnDn(n>2),若ABn的长度为56,则n=_.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,AD=7,点E,F分别在边AD、BC上,且B、F关于过点E的直线对称,如果以CD为直径的圆与EF相切,那么AE= . 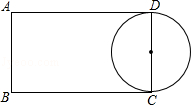
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠MON=45°,点P是∠MON内一点,过点P作PA⊥OM于点A、PB⊥ON于点B,且PB=2 ![]() .取OP的中点C,联结AC并延长,交OB于点D.
.取OP的中点C,联结AC并延长,交OB于点D.
(1)求证:∠ADB=∠OPB;
(2)设PA=x,OD=y,求y关于x的函数解析式;
(3)分别联结AB、BC,当△ABD与△CPB相似时,求PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,在△ABC中,AB=AC,∠BAC=90°.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF. 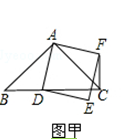
解答下列问题:
(1)当点D在线段BC上时(与点B不重合),如图甲,线段CF、BD之间的位置关系为 , 数量关系为 .
(2)当点D在线段BC的延长线上时,如图乙,①中的结论是否仍然成立,为什么? 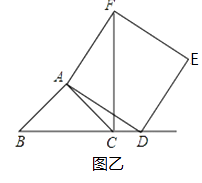
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寒假结束了,为了了解九年级学生寒假体育锻炼情况,王老师调查了九年级所有学生寒假体育锻炼时间,并随即抽取10名学生进行统计,制作出如下统计图表:
编号 | 成绩 | 编号 | 成绩 |
① | B | ⑥ | A |
② | A | ⑦ | B |
③ | B | ⑧ | C |
④ | B | ⑨ | B |
⑤ | C | ⑩ | A |
根据统计图表信息解答下列问题: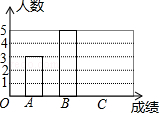
(1)将条形统计图补充完整;
(2)若用扇形统计图来描述10名学生寒假体育锻炼情况,分别求A,B,C三个等级对应的扇形圆心角的度数;
(3)已知这次统计中共有60名学生寒假体育锻炼时间是A等,请你估计这次统计中B等,C等的学生各有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com