
����Ŀ�������ǵ�39��ֲ���ڣ���������ˡ�����ɫʱ�У�������ɫ�������ij��飮ijУΪ������Ӧ��һ���飬�����ڰˡ����꼶��չ���Ļ��У��ί���������꼶�����ڵ�Ͷ���������ͳ�ƣ����Ƴ�����ͼ��ʾ��������������ͳ��ͼ�� 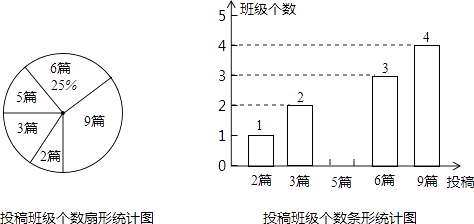
��1��������ͳ��ͼ��Ͷ��3ƪ�İ༶��������Ӧ�����ε�Բ�ĽǵĶ�����
��2�����У�ˡ����꼶��������һ����Ͷ���ƽ��ƪ��������������ͳ��ͼ����������
��3����Ͷ��ƪ������4�����У��ˡ����꼶���������࣬У��ί�������ĸ�����ѡ��������μ�ȫУ�ı��ûᣬ�������б�������״ͼ�ķ��������ѡ���������ò���ͬһ�꼶�ĸ��ʣ�
���𰸡�
��1���⣺�༶�ܸ���Ϊ��3��25%=12�������� ![]() ��360��=60�㣮
��360��=60�㣮
��Ͷ��ƪ��Ϊ3����Ӧ�����ε�Բ�ĽǵĶ���Ϊ60��
��2���⣺Ͷ��5ƪ�İ༶��Ϊ��12��1��2��3��4=2��������
��2+3��2+5��2+6��3+9��4����12=72��12=6��ƪ����
��������ͳ��ͼ��������Ϊ��

��3���⣺����״ͼ���£�
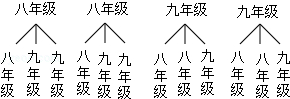 ��
��
�ܹ�12������������ͬһ�꼶����8�������
������ѡ�������ͬһ�꼶�ĸ���Ϊ��8��12= ![]()
����������1������Ͷ��6ƪ�İ༶������3������ռ�ı�����25%�������ܹ��༶����������Ͷ��ƪ��Ϊ3�ı�������360�㼴����⣻��2�����ݼ�Ȩƽ������ʽ�����У�ˣ����꼶��������һ����Ͷ���ƽ��ƪ���������ܹ��༶��������ͬͶ������İ༶����������⣻��3��������״ͼ����Ȼ�����ø��ʵļ��㹫ʽ������⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У�AB��BC��AB=6��BC=4��P�ǡ�ABC�ڲ���һ�����㣬�������PAB=��PBC�����߶�CP������СֵΪ�� �� 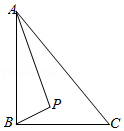
A.![]()
B.2
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=4��AD=7����E��F�ֱ��ڱ�AD��BC�ϣ���B��F���ڹ���E��ֱ�߶Գƣ������CDΪֱ����Բ��EF���У���ôAE= �� 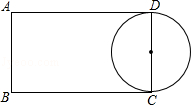
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����MON=45�㣬��P�ǡ�MON��һ�㣬����P��PA��OM�ڵ�A��PB��ON�ڵ�B����PB=2 ![]() ��ȡOP���е�C������AC���ӳ�����OB�ڵ�D��
��ȡOP���е�C������AC���ӳ�����OB�ڵ�D��
��1����֤����ADB=��OPB��
��2����PA=x��OD=y����y����x�ĺ�������ʽ��
��3���ֱ�����AB��BC������ABD���CPB����ʱ����PA�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=4��BC=6����EΪBC���е㣬����ABE��AE�۵���ʹ��B���ھ����ڵ�F��������CF����CF�ij�Ϊ�� �� 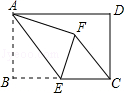
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ף��ڡ�ABC�У�AB=AC����BAC=90�㣮��DΪ����BC��һ���㣬����AD����ADΪһ������AD���Ҳ���������ADEF�� 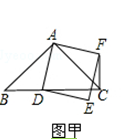
����������⣺
��1������D���߶�BC��ʱ�����B���غϣ�����ͼ�ף��߶�CF��BD֮���λ�ù�ϵΪ �� ������ϵΪ ��
��2������D���߶�BC���ӳ�����ʱ����ͼ�ң����еĽ����Ƿ���Ȼ������Ϊʲô�� 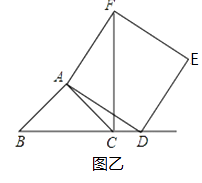
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽƬABCD�У�AB=3cm���ֽ�ֽƬ�۵�ѹƽ��ʹ��A���C�غϣ��ۺ�ΪEF�����sin��BAE= ![]() ����ô�ص����֡�AEF�����Ϊ�� ��
����ô�ص����֡�AEF�����Ϊ�� �� 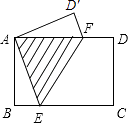
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c����A����1��0����B��3��0����N��2��3�����㣬����y�ύ�ڵ�C��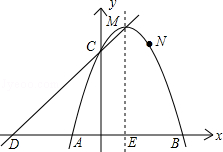
��1����������κ����Ľ���ʽ����д������M����C�����ꣻ
��2����ֱ��y=kx+d����C��M���㣬����x�ύ�ڵ�D����֤���ı���CDAN��ƽ���ı��Σ�
��3����P��������κ����ĶԳ�����һ���㣬��̽�����Ƿ���������ĵ�P��ʹ�Ե�PΪԲ�ĵ�Բ����A��B���㣬������ֱ��CD���У�������ڣ��������P�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ֲij����ɫ�߲ˣ�ȫ���������ڣ�Ϊ��������ڹ�ģ�����о����������߲˵���ֲʵ�������������涨ÿ��ֲ��Ķ�����߲�һ���Բ�����ũ����Ԫ�������飬��ֲĶ��y��Ķ���벹������x��Ԫ��֮�����������ͼ1��ʾ��һ�κ�����ϵ�����Ų�������x�IJ�����������Ҳ�������ӣ���ÿĶ�߲˵�����z��Ԫ������Ӧ���ͣ���z��x֮��Ҳ����������ͼ2��ʾ��һ�κ�����ϵ�� 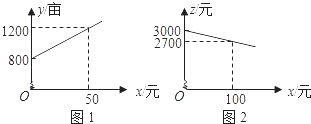
��1��������δ��̨������ʩǰ��������ֲ�����߲˵��������Ϊ���٣�
��2���ֱ����������������ʵʩ����ֲĶ��y��ÿĶ�߲˵�����z��������������x֮��ĺ�����ϵʽ��
��3��Ҫʹȫ�������߲˵�������w��Ԫ���������Ӧ��ÿĶ��������x��Ϊ���٣������������w�����ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com