
【题目】某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植﹣亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系. 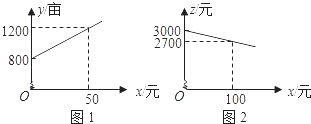
(1)在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(2)分别求出政府补贴政策实施后,种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式;
(3)要使全市这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?并求出总收益w的最大值.
【答案】
(1)解:政府没出台补贴政策前,这种蔬菜的收益额为3000×800=2400000(元)
(2)解:设种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式分别为:
y=kx+800,z=k1x+3000,
分别把点(50,1200),(100,2700)代入得,
50k+800=1200,100k1+3000=2700,
解得:k=8,k1=﹣3,
种植亩数与政府补贴的函数关系为:y=8x+800
每亩蔬菜的收益与政府补贴的函数关系为z=﹣3x+3000(x>0)
(3)解:由题意:
w=yz=(8x+800)(﹣3x+3000)
=﹣24x2+21600x+2400000
=﹣24(x﹣450)2+7260000,
∴当x=450,即政府每亩补贴450元时,总收益额最大,为7260000元
【解析】(1)根据题意可知直接计算这种蔬菜的收益额为3000×800=2400000(元);(2)设种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式分别为:y=kx+800,z=k1x+3000,并根据图象上点的坐标利用待定系数法求函数的解析式即可;(3)表示出蔬菜的总收益w(元)与x之间的关系式,w=﹣24x2+21600x+2400000,利用二次函数最值问题求最大值.


科目:初中数学 来源: 题型:
【题目】今年是第39个植树节,我们提出了“追求绿色时尚,走向绿色文明”的倡议.某校为积极响应这一倡议,立即在八、九年级开展征文活动,校团委对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图. 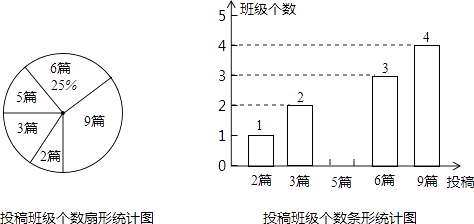
(1)求扇形统计图中投稿3篇的班级个数所对应的扇形的圆心角的度数.
(2)求该校八、九年级各班在这一周内投稿的平均篇数,并将该条形统计图补充完整.
(3)在投稿篇数最多的4个班中,八、九年级各有两个班,校团委准备从这四个班中选出两个班参加全校的表彰会,请你用列表法或画树状图的方法求出所选两个班正好不在同一年级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
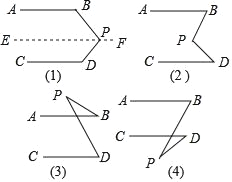
【题目】如图(1),AB∥CD,试求∠BPD与∠B、∠D的数量关系,说明理由.
(1)填空:
解:过点P作EF∥AB,
∴∠B+∠BPE=180°
∵AB∥CD,EF∥AB
∴ (如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∠EPD+ =180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(2)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的数量关系,并说明理由.
(3)观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B、∠D的数量关系,不用说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.

(1)请补全下表:
30° | 45° | 60° | 90° | 120° | 135° | 150° | |
S |
| 1 |
|
(2)填空:
由(1)可以发现正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把菱形的面积S记为S(α).例如:当α=30°时,![]() ;当α=135°时,
;当α=135°时,![]() .由上表可以得到
.由上表可以得到![]() ( ______°);
( ______°);![]() ( ______°),…,由此可以归纳出
( ______°),…,由此可以归纳出![]() .
.
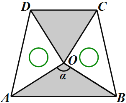
(3) 两块相同的等腰直角三角板按如图的方式放置,AD=![]() ,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某研究机构经过抽样调查,发现当地1500个老年人的养老模式主要有A,B,C,D,E五种,统计结果如图,那么下列说法不正确的是( )
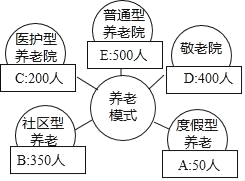
A. 选择A型养老的频率是![]()
B. 可以估计当地30000个老年人中有8000人选择C型养老
C. 样本容量是1500
D. 总体是当地1500个老年人的养老模式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 2 | 5 | 1 | 5 | 4 | 7 | 4 | 3 | 3 | 6 |
根据以上数据,解答下列问题:
(I)直接填空:第10次摸棋子摸到黑棋子的频率为 ;
(Ⅱ)试估算袋中的白棋子数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铁路货运调度站有A、B两个信号灯,在灯这旁停靠着甲、乙、丙三列火车.它们中最长的车长与居中车长之差等于居中车长与最短车长之差,其中乙车的车长居中,最开始的时候,甲、丙两车车尾对齐,且车尾正好位于A信号灯处,而车头则冲着B信号灯的方向,乙车的车尾则位于B信号灯处,车头则冲着A的方向,现在,三列火车同时出发向前行驶,3秒之后三列火车的车头恰好相遇,再过9秒,甲车恰好超过丙车,而丙车也正好完全和乙车错开,请问:甲乙两车从车头相遇直到完全错开一共用了_____秒钟.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com