
����Ŀ���Ķ�����IJ��ϣ�������⣺Ϊ�ⷽ��x2��1��2��5��x2��1��+6=0�����ǿ��Խ���x2��1������һ�����壬Ȼ��x2��1=y����ôԭ���̿ɻ�Ϊy2��5y+6=0�����y1=2��y2=3��
��y=2ʱ��x2��1=2��x2=3��x=��![]() ��
��
��y=3ʱ��x2��1=3��x2=4��x=��2��
��ԭ���̵Ľ�Ϊx1=![]() �� x2=��
�� x2=��![]() �� x3=2��x4=��2��
�� x3=2��x4=��2��
�������ⷽ����������Ԫ����������������Ԫ�����ⷽ�̣���x2+x��2��4��x2+x����12=0��
���𰸡�x1=��3��x2=2��
��������
����y=x2+x����ԭ���̱���Ϊy2��4y��12=0��������ʽ�ֽⷨ���y1=��2��y2=6���ٰ�y=��2��6�ֱ����y=x2+x�õ�����x��һԪ���η��̣�Ȼ�������һԪ���η��̣����ȷ��ԭ���̵Ľ⣮
��y=x2+x����
y2��4y��12=0������y��6����y+2��=0��
��ã�y1=��2��y2=6��
��y1=��2ʱ��x2+x=��2����x2+x+2=0���˷����⣻
��y2=6��ʱ��x2+x=6������x+3����x��2��=0��
��ã�x1=��3��x2=2��
����ԭ���̵Ľ�Ϊx1=��3��x2=2.


 �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У�AB=AC,�ѡ�ABC��A����˳ʱ�뷽����ת�õ���ADE,����BD��CE���ڵ�F��BD��AE�ڵ�G.
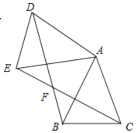
(1)��֤:��AEC�ա�ADB ;
(2)��AB=2,��ACB=67.5����AC��DF ����BD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У����κ���y=��![]() +bx+c��ͼ����A��1��0�����ҵ�x=0��x=5ʱ����Ӧ�ĺ���ֵ��ȣ�һ�κ���y=��x+3����κ���y=��
+bx+c��ͼ����A��1��0�����ҵ�x=0��x=5ʱ����Ӧ�ĺ���ֵ��ȣ�һ�κ���y=��x+3����κ���y=��![]() +bx+c��ͼ��ֱ���B��C���㣬��B�ڵ�һ���ޣ�
+bx+c��ͼ��ֱ���B��C���㣬��B�ڵ�һ���ޣ�
��1������κ���y=��![]() +bx+c�ı���ʽ��
+bx+c�ı���ʽ��
��2������AB����AB�ij���
��3������AC��M���߶�AC���е㣬����B�Ƶ�M��ת180���õ���N������AN��CN���ж��ı���ABCN����״����֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�������Σ�BE��EF��DF��EF��BE��2.5cm��DF��4cm����ôEF�ij�Ϊ�� ��
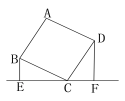
A. 6.5cm B. 6cm C. 5.5cm D. 4cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���E��F��G��H�ֱ��DZ�AB��BC��CD��DA���е㣬����EF��FG��GH��HE����EH��2EF�������н�����ȷ����

A. AB��![]() EF B. AB��2EF C. AB��
EF B. AB��2EF C. AB��![]() EF D. AB��
EF D. AB��![]() EF
EF
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+c��ͼ���һ���֣��Գ�����ֱ��x=1����b2��4ac�� ��b��0����y��x���������С�� ��������2��y1������5��y2�����������ϵ����㣬��y1��y2������4���ж��У���ȷ���ǣ� ��

A. �٢ڢ� B. �٢� C. �٢ۢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ����ཻ�ڵ�0��AC��2��BD��![]() �������ΰ���ͼ��ʽ�۵���ʹ��B���O�غϣ��ۺ�ΪEF���������AEFCD������ǣ� ��
�������ΰ���ͼ��ʽ�۵���ʹ��B���O�غϣ��ۺ�ΪEF���������AEFCD������ǣ� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ����
��ͼ1����֪��ABCΪ�ȱ������Σ���D��E�ֱ��ڱ�AB��AC�ϣ�AD=AE������DC����M��P��N�ֱ�ΪDE��DC��BC���е㣮
��1���۲��������ͼ1�У��߶�PM��PN��������ϵ���� ������MPN�Ķ������� ����
��2��̽��֤�����ѡ�ADE�Ƶ�A��ʱ�뷽����ת��ͼ2��λ�ã�
���жϡ�PMN����״����˵�����ɣ�
�����MPN�Ķ�����
��3����չ����������ABCΪֱ�������Σ���BAC=90�㣬AB=AC=10����DE�ֱ��ڱ�AB��AC�ϣ�AD=AE=4������DC����M��P��N�ֱ�ΪDE��DC��BC���е㣮�ѡ�ADE�Ƶ�A��ƽ����������ת����ͼ3����ֱ��д����PMN��������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�E��F�ǶԽ���BD�����㣬�ҡ�EAF=45��������ADF�Ƶ�A˳ʱ����ת90���õ���ABQ������EQ����֤��
��1��EA�ǡ�QED��ƽ���ߣ�
��2��EF2=BE2+DF2��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com