
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,联结BD与CE交于点F,BD交AE于点G.
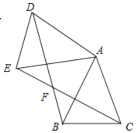
(1)求证:△AEC≌△ADB ;
(2)若AB=2,∠ACB=67.5°,AC∥DF ,求BD的长.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据旋转的性质得:△ABC≌△ADE,且AB=AC,进而得到∠CAE=∠DAB,再根据SAS即可判定△AEC≌△ADB;
(2)根据AB=AC, ∠ACB=67.5°,可求∠BAC=45°,根据AC∥DF ,可得∠DBA=45°,然后判定△ABD为等腰直角三角形.
解:(1)由旋转的性质得:△ABC≌△ADE,且AB=AC,
∴AE=AD,AC=AB,∠BAC=∠DAE,
∴∠BAC+∠BAE=∠DAE+∠BAE,
即∠CAE=∠DAB,
在△AEC和△ADB中,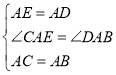 ,
,
∴△AEC≌△ADB(SAS);
(2)∵AB=AC, ∠ACB=67.5°
∴∠BAC=180°-2×67.5°=45°
∵AC∥DF
∴∠DBA=∠BAC=45°
又∵AD=AB
∴△ABD为等腰直角三角形且AB=2
∴BD=![]()


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
(1)点D在边AB上时,请证明:BD=AB﹣AF;
(2)试探索:点D在AB的延长线或反向延长线上时,请在备用图中画出图形,(1)中的结论是否成立?若不成立,请直接写出正确结论(不需要证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC![]()
![]() ,点E是边AD的中点,连接BE交AC于F,BE的延长线交CD的延长线于G.
,点E是边AD的中点,连接BE交AC于F,BE的延长线交CD的延长线于G.
(1)求证:![]() ;
;
(2)若GE=2,BF=3,求线段EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣![]() x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分,而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了,有一种用“因式分解”法产生的密码、方便记忆,其原理是:将一个多项式分解因式,如多项式:![]() 因式分解的结果为
因式分解的结果为![]() ,当
,当![]() 时,
时,![]() 此时可以得到数字密码171920.
此时可以得到数字密码171920.
(1)根据上述方法,当![]() 时,对于多项式
时,对于多项式![]() 分解因式后可以形成哪些数字密码?(写出三个)
分解因式后可以形成哪些数字密码?(写出三个)
(2)若一个直角三角形的周长是24,斜边长为10,其中两条直角边分别为x、y,求出一个由多项式![]() 分解因式后得到的密码(只需一个即可);
分解因式后得到的密码(只需一个即可);
(3)若多项式![]() 因式分解后,利用本题的方法,当
因式分解后,利用本题的方法,当![]() 时可以得到其中一个密码为242834,求m、n的值.
时可以得到其中一个密码为242834,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD在直角坐标系中的位置如图所示,其中边AD和边BC都与x轴平行,边AB和边CD都与y轴平行,且D(2,3),点C的纵坐标是-1,反比例函数y=![]() (k≠0)的图像过点C,与边AB交于点E.
(k≠0)的图像过点C,与边AB交于点E.

(1)求直线OD的表达式和此反比例函数的解析式:
(2)如果点B到y轴的距离是4,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是“人字形”钢架,其中斜梁AB=AC,顶角∠BAC=120°,跨度BC=10m,AD为支柱(即底边BC的中线),两根支撑架DE⊥AB,DF⊥AC,则DE+DF等于( )

A.10mB.5mC.2.5mD.9.5m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,点E,F分别是BC,AC的中点.
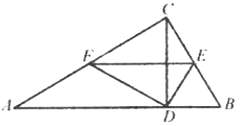
(1)求证:DF⊥DE.
(2)若AC=8,BC=6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料,解答问题:为解方(x2﹣1)2﹣5(x2﹣1)+6=0.我们可以将(x2﹣1)看作一个整体,然后x2﹣1=y,那么原方程可化为y2﹣5y+6=0,解得y1=2,y2=3.
当y=2时,x2﹣1=2,x2=3,x=±![]() ;
;
当y=3时,x2﹣1=3,x2=4,x=±2.
当原方程的解为x1=![]() , x2=﹣
, x2=﹣![]() , x3=2,x4=﹣2.
, x3=2,x4=﹣2.
上述解题方法叫做“换元法”;请利用“换元法”解方程.(x2+x)2﹣4(x2+x)﹣12=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com