
【题目】如图是“人字形”钢架,其中斜梁AB=AC,顶角∠BAC=120°,跨度BC=10m,AD为支柱(即底边BC的中线),两根支撑架DE⊥AB,DF⊥AC,则DE+DF等于( )

A.10mB.5mC.2.5mD.9.5m
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
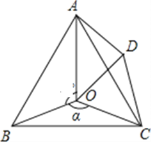
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=130°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机械租赁公司有同一型号的机械设备40套,经过一段时间的经营发现:当每套机械设备的月租金为270元时,恰好全部租出,在此基础上,当每套设备的月租金提高10元时,这种设备就少租一套,且未租出一套设备每月需要支出费用(维护费、管理费等)20元.
(1)设每套设备的月租金为![]() (元),用含
(元),用含![]() 的代数式表示未租出的设备数(套)以及所有未租出设备(套)的支出费用;
的代数式表示未租出的设备数(套)以及所有未租出设备(套)的支出费用;
(2)租赁公司的月收益能否达到11040元?此时应该出租多少套机械设备?每套月租金是多少元?请简要说明理由;
(3)租赁公司的月收益能否在11040元基础上再提高?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,联结BD与CE交于点F,BD交AE于点G.
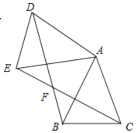
(1)求证:△AEC≌△ADB ;
(2)若AB=2,∠ACB=67.5°,AC∥DF ,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( )

A. 0.5cm B. 1cm C. 1.5cm D. 2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
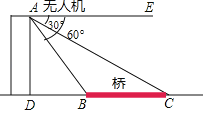
【题目】小亮在某桥附近试飞无人机,如图,为了测量无人机飞行的高度AD,小亮通过操控器指令无人机测得桥头B,C的俯角分别为∠EAB=60°,∠EAC=30°,且D,B,C在同一水平线上.已知桥BC=30米,求无人机飞行的高度AD.(精确到0.01米.参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=﹣![]() +bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣
+bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣![]() +bx+c的图象分别交于B,C两点,点B在第一象限.
+bx+c的图象分别交于B,C两点,点B在第一象限.
(1)求二次函数y=﹣![]() +bx+c的表达式;
+bx+c的表达式;
(2)连接AB,求AB的长;
(3)连接AC,M是线段AC的中点,将点B绕点M旋转180°得到点N,连接AN,CN,判断四边形ABCN的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线相交于点0,AC=2,BD=![]() .将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的面积是( )
.将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的面积是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com