
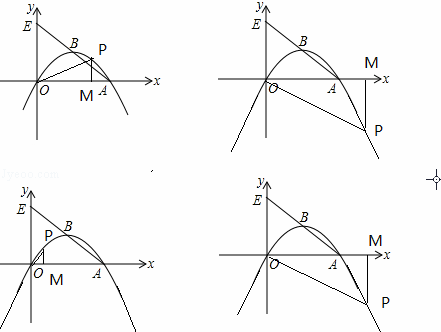
如图,抛物线l1:y=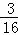 x2平移后过点A(8,0)和原点得到抛物线l2,l2 的顶点为B,对称轴与x轴相交于点C,与原抛物线l1相交于点D,直线AB交y轴于点E.
x2平移后过点A(8,0)和原点得到抛物线l2,l2 的顶点为B,对称轴与x轴相交于点C,与原抛物线l1相交于点D,直线AB交y轴于点E.
(1)求l2的解析式并和阴影部分的面积S阴影;
在l2的对称轴上是否存在一个点F,使得△OEF的周长最小?若存在,求出点F的坐标;若不存在,说明理由;
(3)点P是抛物线l2上一个动点,过P作PM⊥x轴垂足为M,是否存在点P,使得以O、P、M为顶点的三角形与△OAE相似?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
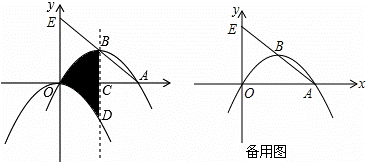
解:(1)设平移后抛物线的解析式y=﹣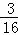 x2+bx,
x2+bx,
将点A(8,0)代入,
得:0=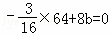 ,
,
解得:b=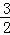 ,∴y=
,∴y=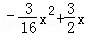 ,
,
顶点B(4,3),
S阴影=OC×CB=4×3=12;
存在,
∵点O与点A关于l2的对称轴对称,
∴连接AE,OF,OF+EF=AE,
此时,点F与点B重合,
∴F(4,3);
(3)存在点P,使得以O、P、M为顶点的三角形与△OAE相似,
设点P(t, ) (t≠0),则:OM=|t|,PM=|
) (t≠0),则:OM=|t|,PM=| |,
|,
设直线AB的解析式为:y=kx+b,
把点A(8,0)和B(4,3)代入可得:
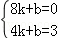 ,
,
解得: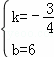 ,
,
∴y=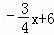 ,当x=0时,y=6,
,当x=0时,y=6,
∴E(0,6),
①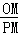 =
=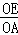 =
=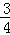 时,
时,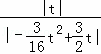 =
=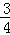 ,
,
∴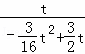 =
=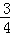 或
或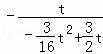 =
=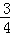 ,
,
解得:t=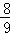 ,或t=
,或t=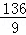 ∴P(
∴P(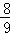 ,
,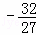 )或P(
)或P(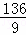 ,
,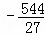 ),
),
②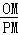 =
=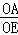 =
=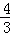 时,
时,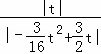 =
=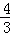 ,
,
∴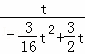 =
=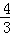 或
或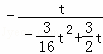 =
=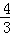 ,
,
解得:t=4或t=12,∴P(4,3)或P(12,﹣9),
∴P1(4,3),P2(12,﹣9),P3(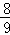 ,
,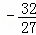 ),P4(
),P4(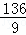 ,
,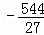 )
)
 .
.


科目:初中数学 来源: 题型:
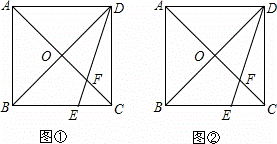
如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE,交AC于点F.
(1)如图①,当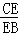 =
= 时,求
时,求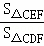 的值;
的值;
(2)如图②,当DE平分∠CDB时,求证:AF= OA.
OA.
查看答案和解析>>
科目:初中数学 来源: 题型:
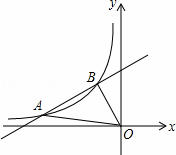
如图,已知一次函数y=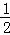 x+b与反比例函数y=
x+b与反比例函数y=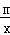 在第二象限的图象交于A(n,
在第二象限的图象交于A(n,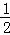 )、B(﹣1,2)两点.
)、B(﹣1,2)两点.
(1)求m、n的值;
根据图象回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(3)△AOB的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧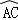 沿弦AC翻折交AB于点D,连接CD.如果∠BAC=20°,则∠BDC=( )
沿弦AC翻折交AB于点D,连接CD.如果∠BAC=20°,则∠BDC=( )
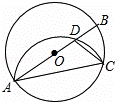
A. 80° B. 70° C. 60° D. 50°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com