
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() .
.
![]() 求证:抛物线总与
求证:抛物线总与![]() 轴有两个不同的交点;
轴有两个不同的交点;
![]() 若
若![]() ,求此抛物线的解析式.
,求此抛物线的解析式.
![]() 已知
已知![]() 轴上两点
轴上两点![]() ,
,![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 有交点,请写出
有交点,请写出![]() 的取值范围.
的取值范围.
【答案】![]() 证明见解析;
证明见解析;![]()
![]() ;
;![]()
![]() .
.
【解析】
(1)、证明△>0即可;(2)、利用抛物线与x轴的交点问题,则![]() 、
、![]() 为方程m
为方程m![]() -8mx+16m-1=0的两根,利用根与系数的关系得到
-8mx+16m-1=0的两根,利用根与系数的关系得到![]() +
+![]() =8,
=8,![]() =
=![]() ,再变形|
,再变形|![]() |=2得到
|=2得到![]() ,然后解出m即可得到抛物线解析式;(3)、先求出抛物线的对称轴为直线x=4,利用函数图象,由于抛物线开口向上,则只要当x=2,y≥0时,抛物线与线段CD有交点,于是得到4m-16m+16m-1≥0,然后解不等式即可.
,然后解出m即可得到抛物线解析式;(3)、先求出抛物线的对称轴为直线x=4,利用函数图象,由于抛物线开口向上,则只要当x=2,y≥0时,抛物线与线段CD有交点,于是得到4m-16m+16m-1≥0,然后解不等式即可.
![]() 、证明:
、证明:![]() , ∵
, ∵![]() ,∴
,∴![]() ,
,
∴抛物线总与![]() 轴有两个不同的交点;
轴有两个不同的交点;
![]() 、根据题意,
、根据题意,![]() 、
、![]() 为方程
为方程![]() 的两根,
的两根,
∴![]() ,
,![]() , ∵
, ∵![]() ,
,
∴![]() , ∴
, ∴![]() , ∴
, ∴![]() ,
,
∴抛物线的解析式为![]() ;
;
![]() 、抛物线的对称轴为直线
、抛物线的对称轴为直线![]() ,
,
∵抛物线开口向上, ∴当![]() ,
,![]() 时,抛物线与线段
时,抛物线与线段![]() 有交点,
有交点,
∴![]() , ∴
, ∴![]() .
.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:
【题目】已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=EC.求证:

(1)△ABC≌△DEF;
(2)FG=CG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若![]() ,
,![]() 是关于
是关于![]() 的方程
的方程![]() 的两个实数根,且
的两个实数根,且![]() (
(![]() 是整数),则称方程
是整数),则称方程![]() 为“偶系二次方程”.如方程
为“偶系二次方程”.如方程![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,都是“偶系二次方程”.
,都是“偶系二次方程”.
![]() 判断方程
判断方程![]() 是否是“偶系二次方程”,并说明理由;
是否是“偶系二次方程”,并说明理由;
![]() 对于任意一个整数
对于任意一个整数![]() ,是否存在实数
,是否存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 是“偶系二次方程”,并说明理由.
是“偶系二次方程”,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮进行百米赛跑,小明比小亮跑得快,如果两人同时起跑,小明肯定赢,现在小明让小亮先跑若干米,图中![]() ,
,![]() 分别表示两人的路程与小明追赶时间的关系.
分别表示两人的路程与小明追赶时间的关系.

(1)哪条线表示小明的路程与时间之间的关系?
(2)小明让小亮先跑了多少米?
(3)谁将赢得这场比赛?
(4)![]() 对应的一次函数表达式中,一次项系数是多少?它的实际意义是什么?
对应的一次函数表达式中,一次项系数是多少?它的实际意义是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B、E、C、F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=13,EC=5,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在
,在![]() 中,
中,![]() 、
、![]() 的平分线相交于点O
的平分线相交于点O
![]() 若
若![]() ,求
,求![]() 的度数;
的度数;
![]() 若
若![]() ,则
,则![]() ______ ;
______ ;
![]() 若
若![]() ,则
,则![]() ______ ;
______ ;
![]() 如图
如图![]() ,在
,在![]() 中的外角平分线相交于点
中的外角平分线相交于点![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
![]() 上面
上面![]() ,
,![]() 两题中的
两题中的![]() 与
与![]() 有怎样的数量关系?
有怎样的数量关系?

查看答案和解析>>
科目:初中数学 来源: 题型:
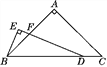
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D在线段BC上,∠EDB=![]() ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE与DF的数量关系,并证明你的结论.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE与DF的数量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com