练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．已知抛物线y=ax2与双曲线y=-$\frac{2}{x}$交点的横坐标大于0，则a的取值范围是（　　）
    A．a＞0B．a＜0C．a＞-2D．a＜-2

    分析 画出函数图象，利用数形结合即可得出抛物线开口向下，由此即可得出a＜0．

    解答 解：依照题意画出函数图象，如图所示．
    ∵双曲线y=-$\frac{2}{x}$的图象在第二、四象限，抛物线y=ax2与双曲线y=-$\frac{2}{x}$交点的横坐标大于0，
    ∴抛物线y=ax2开口向下，
    ∴a＜0．
    故选B．

    点评 本题考查了二次函数图象与系数的关系以及反比例函数的图象，依照题意画出图形，利用数形结合解决问题是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    15．如图：线段AD=8cm，线段AC=BD=6cm，E、F分别是线段AB、CD的中点，EF的长是6cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．已知a2n=4，b2n=9，求an•bn的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．在一个边长为（6$\sqrt{15}$+5$\sqrt{5}$）的正方形内部挖去一个边长为（6$\sqrt{15}$-5$\sqrt{5}$）的正方形，求剩余部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图所示，BO平分∠CBA，CO平分∠ACB，过O作EF∥BC，若AB=12，AC=8，求△AEF的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

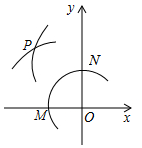    9．如图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交x轴于点M，交y轴于点N，再分别以点M、N为圆心，大于$\frac{1}{2}$MN的长为半径画弧，两弧在第二象限交于点P．若点P的坐标为（2a，b+1），则a与b的数量关系为（　　）
    A．a=bB．2a-b=1C．2a+b=-1D．2a+b=1

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．当x=-3时，分式$\frac{{{x^2}-9}}{x-3}$的值为零；当y＞$\frac{1}{2}$时，分式$\frac{1-2y}{{2{y^2}+3}}$的值为负．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

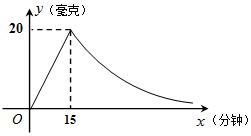    11．为了预防流感，某学校用药熏消毒法对教室进行消毒．已知一瓶药物释放过程中，室内每立方米空气中的含药量y（毫克）与时间x（分钟）成正比例；药物释放完毕后，y与x成反比例，如图所示．根据图中提供的信息，解答下列问题：
    （1）写出倾倒一瓶药物后，从药物释放开始，y与x之间的两个函数关系式及相应的自变量取值范围；
    （2）据测定，当空气中每立方米的含药量不低于8毫克时，消毒有效，那么倾倒一瓶药物后，从药物释放开始，有效消毒时间是多少分钟？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．某商场购进一批西服，进价为每套250元，原定每套以290元的价格销售，这样每天可销售200套，如果每套比原销售价降低10元销售，则每天可多销售100套，该商场为了确定销售价格，作了如下测算，请你参加测算，并由此归纳得出结论．（每套西服的利润=每套西服的销售价-每套西服的进价）．
    （1）按原销售价销售，每天可获利润8000元；
    （2）若每套降低10元销售，每天可获利润9000元；
    （3）如果每套销售价降低10元，每天就多销售100套，每套销售价降低20元，每天就多销售200套，按这种方式：
    若每套降低10x元（0≤x≤4，x为正整数）．
    ①则每套的销售价格为（290-10x）元（用代数式表示）；
    ②则每天可销售（200+100x）套西服（用代数式表示）；
    ③则每天共可以获利润（40-10x）（200+100x）元（用代数式表示）
    ④根据以上的测算，如果你是该商场的经理，你将如何确定商场的销售方案，使每天的获利最大？

    查看答案和解析>>

    同步练习册答案