
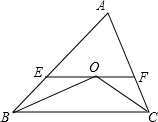
 如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若AB=12,AC=8,求△AEF的周长.
如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若AB=12,AC=8,求△AEF的周长. 分析 根据角平分线的定义可得∠OBE=∠OBC,∠OCF=∠OCB,再根据两直线平行,内错角相等可得∠OBC=∠BOE,∠OCB=∠COF,然后求出∠OBE=∠BOE,∠OCF=∠COF,再根据等角对等边可得OE=BE,OF=CF,即可得证.
解答 解:∵BO平分∠CBA,
∴∠EBO=∠OBC,
∵CO平分∠ACB,
∴∠FCO=∠OCB,
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=OE,CF=OF,
∴△AEF的周长=AE+OE+OF+AF=AE+BE+CF+AF=AB+AC,
∵AB=12,AC=8,
∴C△AEF=12+8=20.
点评 本题考查了等腰三角形的判定与性质,平行线的性质,主要利用了角平分线的定义,等角对等边的性质,两直线平行,内错角相等的性质,熟记各性质是解题的关键


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 数a,b在数轴上对应点A,B的位置如图所示,且|a|=2,b是16的一个平方根,求式子|a+b|-$\sqrt{{a}^{2}}$-$\root{3}{(a-b)^{3}}$的值.
数a,b在数轴上对应点A,B的位置如图所示,且|a|=2,b是16的一个平方根,求式子|a+b|-$\sqrt{{a}^{2}}$-$\root{3}{(a-b)^{3}}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
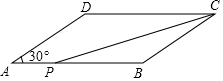 如图,在?ABCD中,AB=8cm,BC=6cm,∠A=30°,点P从点A出发沿线段AB以1m/s的速度向B点移动.
如图,在?ABCD中,AB=8cm,BC=6cm,∠A=30°,点P从点A出发沿线段AB以1m/s的速度向B点移动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>0 | B. | a<0 | C. | a>-2 | D. | a<-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
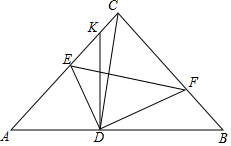 如图,已知在等腰Rt△ABC中,∠C=90°,AB=6,若将△ABC翻折,且点C落在AB边上点D处,折痕EF分别交边AC,BC于点E和点F,过点D作DK⊥AB,交射线AC于点K.
如图,已知在等腰Rt△ABC中,∠C=90°,AB=6,若将△ABC翻折,且点C落在AB边上点D处,折痕EF分别交边AC,BC于点E和点F,过点D作DK⊥AB,交射线AC于点K.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com