
【题目】如图,正方形ABCD的四个顶点A、B、C、D正好分别在四条平行线l1、l3、l4、l2上.若从上到下每两条平行线间的距离都是2cm,则正方形ABCD的面积为cm2 . 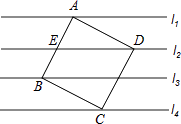
【答案】20
【解析】解:作EF⊥l2 , 交l1于E点,交l4于F点. 
∵l1∥l2∥l3∥l4 , EF⊥l2 ,
∴EF⊥l1 , EF⊥l4 ,
即∠AED=∠DFC=90°.
∵四边形ABCD为正方形,
∴∠ADC=90°.
∴∠ADE+∠CDF=90°.
又∵∠ADE+∠DAE=90°,
∴∠CDF=∠DAE,
在△ADE与△DCF中,  ,
,
∴△ADE≌△DCF,
∴CF=DE=2.
∵DF=4,
∴CD2=22+42=20,
即正方形ABCD的面积为20cm2 .
所以答案是:20.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】端午节前夕,小东的父母准备购买若干个粽子和咸鸭蛋(每个粽子的价格相同,每个咸鸭蛋的价格相同).已知粽子的价格比咸鸭蛋的价格贵1.8元,花30元购买粽子的个数与花12元购买咸鸭蛋的个数相同,求粽子与咸鸭蛋的价格各多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
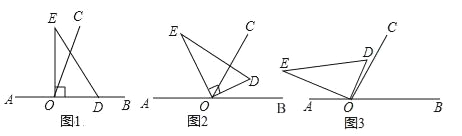
【题目】以直线AB上一点O为端点作射线 OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD= ![]() ∠AOE,求∠BOD的度数?
∠AOE,求∠BOD的度数?
查看答案和解析>>
科目:初中数学 来源: 题型:
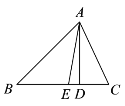
【题目】如图,在△ABC 中,∠C=65°,AD 为 BC 边上的高.
(1)求∠CAD 的度数;
(2)若∠B=45°,AE 平分∠BAC,求∠EAD 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1) 如图1,当∠BOC=70°时,求∠DOE的度数.
(2) 如图2,当射线OC在∠AOB内绕点O旋转时,∠DOE的大小是否发生变化?说明理由.
(3) 当射线OC在∠AOB外绕点O旋转且∠AOC为钝角时,画出图形,直接写出相应的∠DOE的度数.(不必写出过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
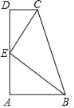
【题目】如图,AB∥CD,∠A=90°,E是AD边中点,CE平分∠BCD.
(1)求证:BE平分∠ABC;
(2)若AB=2,CD=1,求BC长;
(3)若△BCE的面积为6,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小亮从家步行到公交车站台,乘公交车去学校. 图中的折线表示小亮的离家距离s(km)与所花时间t(min)之间的函数关系. 下列说法错误的是

A. 他离家8km共用了30min B. 公交车的速度是350m/min
C. 他步行的速度是100m/min D. 他等公交车时间为6min
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com