
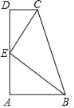
【题目】如图,AB∥CD,∠A=90°,E是AD边中点,CE平分∠BCD.
(1)求证:BE平分∠ABC;
(2)若AB=2,CD=1,求BC长;
(3)若△BCE的面积为6,求四边形ABCD的面积.
【答案】(1)证明见解析;(2)BC=3;(3)12.
【解析】
(1)作EM⊥BC垂足为M,根据角平分线的判定与性质即可得证;
(2)通过HL证明Rt△CDE≌Rt△CME与Rt△BAE≌Rt△BNE,可得CM=CD,BM=AB,然后相加即可得解;
(3)根据(2)可知Rt△CDE≌Rt△CME与Rt△BAE≌Rt△BNE,则四边形ABCD的面积为△BCE面积的2倍.
(1)证明:作EM⊥BC垂足为M,
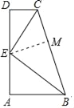
∵EC平分∠DCB,ED⊥CD,EM⊥BC,
∴ED=EM,
∵AE=ED,
∴EA=EM,
∵EA⊥AB,EM⊥BC,
∴EB平分∠ABC;
(2)证明:由(1)可知:AE=EM=ED,
在Rt△DEC和Rt△CEM中,
![]() ,
,
∴△ECD≌△ECM(HL))
∴DC=CM,
同理可证:AB=BM,
∴BC=CM+MM=CD+AB=3;
(3)解:由(2)可知:△ECD≌△ECM(HL),
∴S△ECD=S△ECM,同法可证:S△EBM=S△EBA,
∴S四边形ABCD=2S△BEC,
∵△BCE的面积为6,
∴四边形ABCD的面积为12.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30o,点A1、A2、A3 在射线ON上,点B1、B2、B3…..在射线OM上,△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形,若OA1=l,则△A6B6A7 的边长为【 】

A.6 B.12 C.32 D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的四个顶点A、B、C、D正好分别在四条平行线l1、l3、l4、l2上.若从上到下每两条平行线间的距离都是2cm,则正方形ABCD的面积为cm2 . 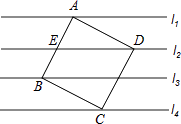
查看答案和解析>>
科目:初中数学 来源: 题型:
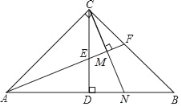
【题目】在Rt△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线AF交CD于点E,交BC于F,CM⊥AF于M,CM的延长线交AB于点N.
(1)求证:EM=FM;
(2)求证:AC=AN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,进价是20元,根据市场调查:在一段时间内,销售单价是30元时,销售量是500件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
销售单价(元) | x |
销售量y(件) | |
销售玩具获得利润w(元) |
(2)在(1)问条件下,若商场获得了8000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具车规定该品牌玩具销售单价不低于35元,且商场要完成不少于350件的销售任务,求商场销售该品牌服装获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”长假期间,小张和小李决定骑自行车外出旅游,两人相约一早从各自家中出发,已知两家相距10千米,小张出发必过小李家.
(1)若两人同时出发,小张车速为20千米,小李车速为15千米,经过多少小时能相遇?
(2)若小李的车速为10千米,小张提前20分钟出发,两人商定小李出发后半小时二人相遇,则小张的车速应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若数a使关于x的不等式组 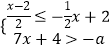 有且仅有四个整数解,且使关于y的分式方程
有且仅有四个整数解,且使关于y的分式方程 ![]() +
+ ![]() =2有非负数解,则所以满足条件的整数a的值之和是( )
=2有非负数解,则所以满足条件的整数a的值之和是( )
A.3
B.1
C.0
D.﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.
(1)求∠E的度数.
(2)请猜想∠A与∠E之间的数量关系,请说明理由.
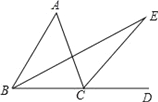
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com