
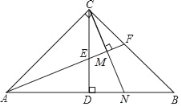
【题目】在Rt△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线AF交CD于点E,交BC于F,CM⊥AF于M,CM的延长线交AB于点N.
(1)求证:EM=FM;
(2)求证:AC=AN.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据题意可得∠AED+∠DAE=90°,∠CFE+∠CAE=90°,因为∠BAC的平分线AF交CD于E,所以∠DAE=∠CAE,即∠AED=∠CFE,然后根据等腰三角形判定与性质即可得证;
(2)通过“角边角”证明△AMN≌△AMC,即可得AC=AN.
(1)证明:∵∠ACB=90°,CD⊥AB,
∴∠ADC=90°,
∴∠AED+∠DAE=90°,∠CFE+∠CAE=90°,
又∵∠BAC的平分线AF交CD于E,
∴∠DAE=∠CAE,
∴∠AED=∠CFE,
又∵∠AED=∠CEF,
∴∠CEF=∠CFE,
又∵CM⊥AF,
∴EM=FM.
(2)证明:∵CN⊥AF,
∴∠AMC=∠AMN=90°,
在△AMN和△AMC中,
 ,
,
∴△AMN≌△AMC(SAS),
∴AC=AN.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】新化到长沙的距离约为200km,小王开着小轿车,张师傅开着大货车都从新化去长沙,小王比张师傅晚出发20分钟,最后两车同时到达长沙.已知小轿车的速度是大货车速度的1.2倍,求小轿车和大货车的速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
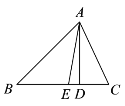
【题目】如图,在△ABC 中,∠C=65°,AD 为 BC 边上的高.
(1)求∠CAD 的度数;
(2)若∠B=45°,AE 平分∠BAC,求∠EAD 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知数轴上点A表示的数为8,B是数轴上一点,且AB=22.动点P从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数____,点P表示的数____(用含t的代数式表示);
(2)若动点Q从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?(列一元一次方程解应用题)
(3)若动点Q从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问 秒时P、Q之间的距离恰好等于2(直接写出答案)
(4)思考在点P的运动过程中,若M为AP的中点,N为PB的中点.线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
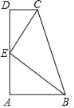
【题目】如图,AB∥CD,∠A=90°,E是AD边中点,CE平分∠BCD.
(1)求证:BE平分∠ABC;
(2)若AB=2,CD=1,求BC长;
(3)若△BCE的面积为6,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐数量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A、B、C、D、E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题: 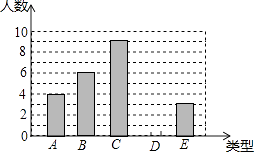
(1)补全条形统计图;
(2)求这30名职工捐书本数的平均数、众数和中位数;
(3)估计该单位750名职工共捐书多少本?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com