
【题目】某商场经营某种品牌的玩具,进价是20元,根据市场调查:在一段时间内,销售单价是30元时,销售量是500件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
销售单价(元) | x |
销售量y(件) | |
销售玩具获得利润w(元) |
(2)在(1)问条件下,若商场获得了8000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具车规定该品牌玩具销售单价不低于35元,且商场要完成不少于350件的销售任务,求商场销售该品牌服装获得的最大利润是多少?
【答案】
(1)﹣10x+800;﹣10x2+1000x﹣16000
(2)解:根据题意,得:﹣10x2+1000x﹣16000=8000,
整理,得:x2﹣100x+2400=0,
解得:x=40或x=60,
∵x>40,
∴x=60,
答:该玩具销售单价x应定为60元;
(3)解:由题意知 ![]() ,
,
解得:35≤x≤45,
∵w=﹣10x2+1000x﹣16000=﹣10(x﹣50)2+9000,
∴当x<50时,w随x的增大而增大,
∴当x=45时,w取得最大值,最大值为﹣10(45﹣50)2+9000=8750,
答:商场销售该品牌服装获得的最大利润是8750元.
【解析】解:(1)由题意,得:y=500﹣10(x﹣30)=﹣10x+800, w=(﹣10x+800)(x﹣20)=﹣10x2+1000x﹣16000.
故答案为:﹣10x+800,﹣10x2+1000x﹣16000.
(1)根据销售量与销售单价之间的变化关系就可以直接求出y与x之间的关系式;根据销售问题的利润=售价﹣进价就可以表示出w与x之间的关系;(2)根据以上关于利润的相等关系列方程求解可得;(3)根据销售单价不低于35元,销售量不少于350件建立不等式组求得x的范围,将函数解析式配方成顶点式,结合函数性质和x的范围求出其最大值即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图的数阵是由88个偶数组成:
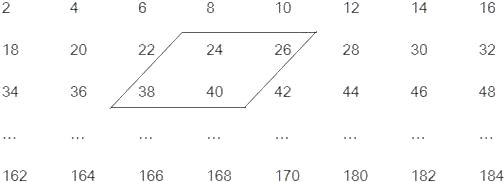
(1)观察数阵中平行四边形框内的四个数之间的关系,在数阵中任意作一个相同的平行四边形框圈出四个数,设其中最小的数为x,那么其他三个数怎样表示?
(2)甲同学这样圈出的四个数的和为432,你能求出这四个数吗?
(3)乙同学想用这样的框圈出和为172的四个数,可能吗?
(4)你能用这样的框圈出和为352的四个数吗?若能,请写出这四个数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1) 如图1,当∠BOC=70°时,求∠DOE的度数.
(2) 如图2,当射线OC在∠AOB内绕点O旋转时,∠DOE的大小是否发生变化?说明理由.
(3) 当射线OC在∠AOB外绕点O旋转且∠AOC为钝角时,画出图形,直接写出相应的∠DOE的度数.(不必写出过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的两条对角线相交于点O,过点A作AG⊥BD分别交BD、BC于点G、E. 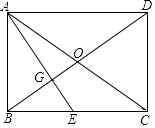
(1)求证:BE2=EGEA;
(2)连接CG,若BE=CE,求证:∠ECG=∠EAC. 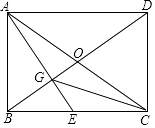
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠A=90°,E是AD边中点,CE平分∠BCD.
(1)求证:BE平分∠ABC;
(2)若AB=2,CD=1,求BC长;
(3)若△BCE的面积为6,求四边形ABCD的面积.
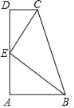
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
我们可以通过以下方法求代数式x2+6x+5的最小值.
x2+6x+5=x2+2x3+32﹣32+5=(x+3)2﹣4,
∵(x+3)2≥0
∴当x=﹣3时,x2+6x+5有最小值﹣4.
请根据上述方法,解答下列问题:
(Ⅰ)x2+4x﹣1=x2+2x2+22﹣22﹣1=(x+a)2+b,则ab的值是_____;
(Ⅱ)求证:无论x取何值,代数式x2+2![]() x+7的值都是正数;
x+7的值都是正数;
(Ⅲ)若代数式2x2+kx+7的最小值为2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知等腰三角形的一边长等于8cm,一边长等于9cm,求它的周长;
(2)等腰三角形的一边长等于6cm,周长等于28cm,求其他两边的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com