
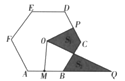
【题目】如图在正六边形![]() 中,有两点
中,有两点![]() 同时、同速从
同时、同速从![]() 中点
中点![]() 出发,P沿
出发,P沿![]() 方向运动,Q点沿
方向运动,Q点沿![]() 方向指向运动,10秒后,两点与多边形中心连线及多边形(延长线)所围成图形的面积如图(阴影部分的面积)有两部分为
方向指向运动,10秒后,两点与多边形中心连线及多边形(延长线)所围成图形的面积如图(阴影部分的面积)有两部分为![]() ,则
,则![]() 之间的数量关系是( )
之间的数量关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
如图,连接OB,OC,作OW⊥BC于W,OT⊥CD于T.因为点P,Q同时,同速从AB中点M出发,所以MQ=MB+BC+PC,推出![]() MQOM=
MQOM=![]() (BM+BC+PC)OM及BC= BG+CG推出S△OMQ=S△OBM+S△OBG+S△OGC+S△OCP=S△OBM+S△OBG+S2,再根据S1=S△OGC+S△OCP,推出S1=S2.
(BM+BC+PC)OM及BC= BG+CG推出S△OMQ=S△OBM+S△OBG+S△OGC+S△OCP=S△OBM+S△OBG+S2,再根据S1=S△OGC+S△OCP,推出S1=S2.
如图,连接OB,OC,作OW⊥BC于W,OT⊥CD于T.
在正六边形ABCDEF中,
∵AM=BM,
∴OM⊥AB,
∵OW⊥BC,OT⊥CD,
∴OM=OW=OT,
∵点P,Q同时,同速从AB中点M出发,
∴MQ=MB+BC+PC,
∴![]() MQOM=
MQOM=![]() (BM+BC+PC)OM,
(BM+BC+PC)OM,
又BC=BG+CG
∴S△OMQ=S△OBM+S△OBG+S△OGC+S△OCP=S△OBM+S△OBG+S2,
∵S1=S△OGC+S△OCP,
∴S1=S2.
故选:C.


科目:初中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的项点为
的项点为![]() ,交
,交![]() 轴于
轴于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点左侧),且
点左侧),且![]() .
.
(1)求抛物线![]() 的函数解析式;
的函数解析式;
(2)过点![]() 的直线交抛物线于点
的直线交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() 的面积被
的面积被![]() 轴分为1: 4两个部分,求直线
轴分为1: 4两个部分,求直线![]() 的解析式;
的解析式;
(3)在(2)的情况下,将抛物线![]() 绕点
绕点![]() 逆时针旋转180°得到抛物线
逆时针旋转180°得到抛物线![]() ,点
,点![]() 为抛物线
为抛物线![]() 上一点,当点
上一点,当点![]() 的横坐标为何值时,
的横坐标为何值时,![]() 为直角三角形?
为直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列要求,解答相关问题:
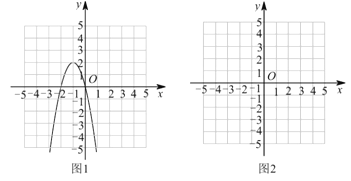
(1)请补全以下求不等式![]() 的解集的过程:
的解集的过程:
①构造函数,画出图象:根据不等式特征构造二次函数![]() ;抛物线的对称轴为_________,开口向下,顶点坐标为__________,与
;抛物线的对称轴为_________,开口向下,顶点坐标为__________,与![]() 轴的交点是_________,用三点法画出二次函数
轴的交点是_________,用三点法画出二次函数![]() 的图象如图1所示;
的图象如图1所示;
②数形结合,求得界点:当![]() 时,求得方程
时,求得方程![]() 的解为___________;
的解为___________;
③借助图象,写出解集:由图象可得不等式![]() 的解集为_________.
的解集为_________.
(2)利用(1)中求不等式解集的方法步骤,求不等式![]() 的解集.
的解集.
①构造函数,画出![]() 的图象(在图2中画出);
的图象(在图2中画出);
②数形结合,求得界点:当![]() __________时,求得方程
__________时,求得方程![]() 的解为__________;
的解为__________;
③借助图象,写出解集.由图2知,不等式![]() 的解集是__________.
的解集是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
(1)求条形图中被遮盖的数,并写出册数的中位数;
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:
销售方式 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 1000 | 2000 |
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润![]() 元与精加工的蔬菜吨数
元与精加工的蔬菜吨数![]() 之间的函数关系式;
之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为鼓励市民节约用气,对居民管道天然气实行两档阶梯式收费,年用天然气量310立方米及以下为第一档;年用天然气量超出310立方米为第二档,某户应交天然气费![]() (元)与年用天然气量
(元)与年用天然气量![]() (立方米)的关系如图所示,观察图像并回答问题:
(立方米)的关系如图所示,观察图像并回答问题:
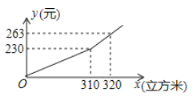
(1)求![]() 与
与![]() 之间的函数解析式并写出自变量
之间的函数解析式并写出自变量![]() 的取值范围;
的取值范围;
(2)嘉琪家2018年天然气费为1029元,求嘉琪家2018年使用天然气量是否超出310立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小兰用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点DE为圆心,大于DE的一半长为半径作弧两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K使K和B在AC的两侧;
所以BH就是所求作的高.其中顺序正确的作图步骤是( )

A.①②③④B.④③①②C.②④③①D.④③②①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OEOP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
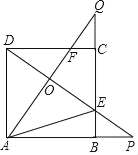
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数 y=ax2+bx+c 的图象与 x 轴的交点的横坐标分别为-1,3,则:
①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意 x 均有 ax2+bx≥a+b,其中结论正确的个数有( )
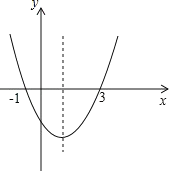
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com