
����Ŀ�����Ķ����ϣ���ƽ��ֱ������ϵ�У���P��x0��y0����ֱ��Ax+By+C��0�ľ��빫ʽ��![]()
�磺���P��1��2����ֱ��y����![]() x+1�ľ���d
x+1�ľ���d
�⣺��ֱ�߽���ʽ����Ϊ4x+3y��3��0����A��4��B��3��C����3
����![]()
��������⣩��ֱ֪��l1�Ľ���ʽ��y��-![]() x+1
x+1
��1������P������Ϊ��1����2�������P��ֱ��l1�ľ������� ����
��2����ֱ��l2��ֱ��l1ƽ�У�������ƽ����ľ�����![]() �������ֱ��l2�Ľ���ʽ��
�������ֱ��l2�Ľ���ʽ��
���𰸡���1��![]() ����2��
����2��![]() ��
��![]()
��������
(1)������Ŀ��֪�ĵ㵽ֱ��֮��ľ��빫ʽ�����빫ʽ�������.
(2)����ֱ��l2��ֱ��l1ƽ�У�����ֱ��l2�Ľ���ʽΪy��![]() x+b����ֱ��l1��ȡһ��P��0��1�������ݵ㵽ֱ�ߵľ��빫ʽ�ó���P��ֱ��l1�ľ�����
x+b����ֱ��l1��ȡһ��P��0��1�������ݵ㵽ֱ�ߵľ��빫ʽ�ó���P��ֱ��l1�ľ�����![]() ���г�����b�ķ��̣��ⷽ�̼���.
���г�����b�ķ��̣��ⷽ�̼���.
�⣺��1����ֱ��l1�Ľ���ʽ��y��![]() x+1��
x+1��
��ֱ�߽���ʽ����Ϊx+2y��2��0��
��A��1��B��2��C����2��
���P��1����2����ֱ��l1�ľ�����d��![]() ��
��
�ʴ�Ϊ![]() ��
��
��2����ֱ��l2��ֱ��l1ƽ�У�ֱ��l1�Ľ���ʽ��y��![]() x+1��
x+1��
�����ֱ��l2�Ľ���ʽΪy��![]() x+b����x+2y��2b��0��
x+b����x+2y��2b��0��
��ֱ��l1��ȡһ��P��0��1�������P��ֱ��l1�ľ�����![]() ��
��
��![]() ��
��
��|2��2b|��5��
���b��![]() ��
��![]() ��
��
��ֱ��l2�Ľ���ʽΪy��![]() x
x![]() ��y��
��y��![]() x+
x+![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ף�л���������70���꣬ij�о�����չ���Һ�������ɳ��������ݽ�������ij��ѧ���μӱ�Уѡ������40��ѡ�ֵijɼ�������Ϊ100�֣��÷�Ϊ�������������֣����Ϊ75�֣��ֳ����飬�����������в�������ͳ��ͼ����
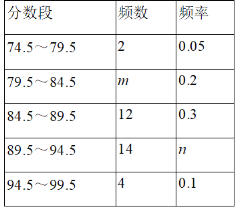
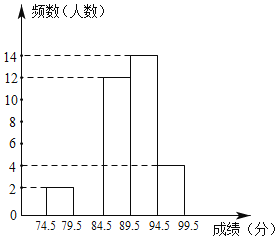
��1������m���� ����n���� ����
��2������ͼ�в�ȫƵ��ֱ��ͼ��
��3����ͬѧ�ı����ɼ���40λ����ѡ�ֳɼ�����λ�����ݴ��Ʋ����ijɼ������� ���������ڣ�
��4��ѡ�����У��ɼ���94.5�����ϵ�ѡ�֣�������Ů����ռһ�룬ѧУ�������ȷ��2��ѡ�ֲμ�ȫ�о����������оٷ�����״ͼ����ǡ����һ��������һ��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
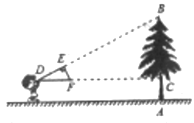
����Ŀ����ͼ��С��ͬѧ�����Ƶ�ֱ��������ֽ��DEF�������ĸ߶�AB���������Լ���λ�ã��跨ʹб��DF����ˮƽ�����ұ�DE���B��ͬһֱ���ϣ���ֽ֪�������ֱ�DZ�DE=0.4m��EF=0.2m����ñ�DF�����ĸ߶�AC=1.5m��CD=8m�������ߡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
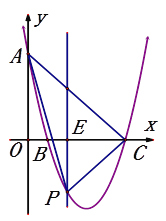
����Ŀ����ƽ��ֱ������ϵ�У�������![]() ��y��Ľ���ΪA����x���������ֱ��ڵ�B��b��0����C��c��0��.
��y��Ľ���ΪA����x���������ֱ��ڵ�B��b��0����C��c��0��.
��1����b=1ʱ������������Ӧ�ĺ�������ʽ��
��2����b=1ʱ����ͼ��E��t��0�����߶�BC�ϵ�һ����,����E��ƽ����y���ֱ��l�������ߵĽ���ΪP�����APC��������ֵ��
��3����c =b+ n.ʱ����nΪ������.�߶�BC�������˵㣩������ֻ�������ĺ���������������b��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�BC��9����ABC��ƽ����BF��AC�ڵ�F����D����E�ֱ��DZ�AB��AC�ϵĵ㣬��![]() ����BD��DE��ֵΪ��������
����BD��DE��ֵΪ��������
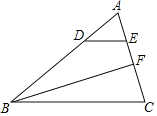
A.3B.3��5C.4D.4��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
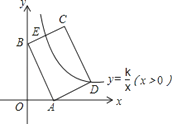
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABCD�ı�AB��BC=3��2����A��3��0����B��0��6���ֱ���x�ᣬy���ϣ�����������y=![]() ��x��0����ͼ����D�������BC���ڵ�E�����E������Ϊ__��
��x��0����ͼ����D�������BC���ڵ�E�����E������Ϊ__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1�������κ���y��ax2��bx��a��0����ͼ����x�ᡢֱ��y��x�Ľ���ֱ�Ϊ��A(4��0)��B(5��5)��

��1��a���� ����b���� ������AOB���� ������
��2������AB����P����������һ�㣨���ڵ�A�����ҡ�PBO����OBA�����P�������� ����
��3����ͼ��2������C��D���߶�OB�ϵĶ��㣬��CD��2![]() �����C�ĺ�����Ϊm��
�����C�ĺ�����Ϊm��
�ٹ���C��D�ֱ���x��Ĵ��ߣ����������ཻ�ڵ�F��E������EF����CF+DEȡ�����ֵʱ����m��ֵ���ж��ı���CDEF����״��
������AC��AD����mΪ��ֵʱ��AC+ADȡ����Сֵ������������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��C��D������ֱ��ǣ�1��7������1��1������4��1������6��1������C��D��EΪ���������������ABC���ƣ����E�����겻������

A����6��0�� B����6��3�� C����6��5�� D����4��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�����
�У�����![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() ���ڵ�A(3,m).
���ڵ�A(3,m).
��1����k��m��ֵ��
��2����֪��P(n��n)(n>0)������P��ƽ����![]() ���ֱ�ߣ���ֱ��y=x-2�ڵ�M������P��ƽ����y���ֱ�ߣ�������
���ֱ�ߣ���ֱ��y=x-2�ڵ�M������P��ƽ����y���ֱ�ߣ�������![]() ��ͼ���ڵ�N.
��ͼ���ڵ�N.
�ٵ�n=1ʱ���ж��߶�PM��PN��������ϵ����˵�����ɣ�
����PN��PM����Ϻ�����ͼ��ֱ��д��n��ȡֵ��Χ.
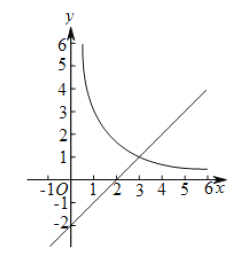
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com