
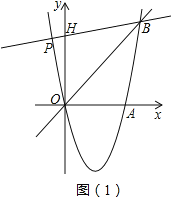
【题目】如图(1),二次函数y=ax2﹣bx(a≠0)的图象与x轴、直线y=x的交点分别为点A(4,0)、B(5,5).

(1)a= ,b= ,∠AOB= °;
(2)连接AB,点P是抛物线上一点(异于点A),且∠PBO=∠OBA,求点P的坐标 ;
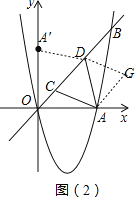
(3)如图(2),点C、D是线段OB上的动点,且CD=2![]() .设点C的横坐标为m.
.设点C的横坐标为m.
①过点C、D分别作x轴的垂线,与抛物线相交于点F、E,连接EF.当CF+DE取得最大值时,求m的值并判断四边形CDEF的形状;
②连接AC、AD,求m为何值时,AC+AD取得最小值,并求出这个最小值.
【答案】(1)1,4,45°;(2)(﹣![]() ,
,![]() );(3)①m=
);(3)①m=![]() ,四边形CDEF为平行四边形;②m=
,四边形CDEF为平行四边形;②m=![]() ,2
,2![]()
【解析】
(1)将点A、B的坐标代入二次函数表达式,即可求解;
(2)证明△HOB≌△AOB(AAS),得OA=OH=4,即点H(0,4),即可求解;
(3)①则CF+DE=m﹣m2+4m+(m+2)﹣[(m+2)2﹣4(m+2)]=﹣2m2+6m+6,即可求解;
②如图所示,过点A作CD的平行线,过点D作AC的平行线,交于点G,则四边形ACDG是平行四边形,当A'、D、G三点共线时,A'D+DG=A'G最短,即可求解.
(1)将点A、B的坐标代入二次函数表达式得:![]() ,解得:
,解得:![]() ,
,
故二次函数表达式为:y=x2+4x,
∵点O,B在直线y=x上,
∴OB平分∠xOy,
∴∠AOB=45;
故:答案为:1,4,45°;
(2)设直线BP交y轴于点H,
∵∠HOB=∠AOB=45°,∠PBO=∠OBA,BO=BO,
∴△HOB≌△AOB(AAS),
∴OA=OH=4,即点H(0,4),
则直线PB的表达式为:y=kx+4,将点B坐标代入上式并解得:
直线PB的表达式为:y=![]() x+4,
x+4,
将上式与二次函数表达式联立并解得:x=5或﹣![]() (舍去正值),
(舍去正值),
则点P(﹣![]() ,
,![]() );
);
(3)①由题意得:直线OB的表达式为:y=x,
设点C(m,m),CD=2![]() ,直线OB的倾斜角为45度,则点D(m+2,m+2),
,直线OB的倾斜角为45度,则点D(m+2,m+2),
则点F(m,m2﹣4m),点E[(m+2),(m+2)2﹣4(m+2)],
则CF+DE=m﹣m2+4m+(m+2)﹣[(m+2)2﹣4(m+2)]=﹣2m2+6m+6,
∵﹣2<0,故CF+DE有最大值,此时,m=![]() ,
,
则点C、F、D、E的坐标分别为(![]() ,
,![]() )、(
)、(![]() ,﹣
,﹣![]() )、(
)、(![]() ,
,![]() )、(
)、(![]() ,﹣
,﹣![]() ),
),
则CF=DE=![]() ,CF∥ED,
,CF∥ED,
故四边形CDEF为平行四边形;
②如图所示,过点A作CD的平行线,过点D作AC的平行线,交于点G,则四边形ACDG是平行四边形,
∴AC=DG,
作点A关于直线OB的对称点A'(0,4),连接A'D,则A'D=AD,
∴当A'、D、G三点共线时,A'D+DG=A'G最短,此时AC+AD最短,
∵A(4,0),AG=CD=2![]() ,
,
则点G(6,2),
则AC+AD最小值=A'G=![]() =2
=2![]() ;
;


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
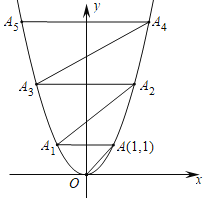
【题目】在平面直角坐标系中,抛物线y=x2如图所示,已知A点坐标为(1,1),过点A作AA1∥x轴交抛物线于点A1,过点A1作A1A2∥OA交抛物线于点A2,过点A2作A2A3∥x轴交抛物线于点A3,过点A3作A3A4∥OA交抛物线于点A4,过点A4作A4A5∥x轴交抛物线于点A5,则点A5的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系内,抛物线y=x2﹣bx+6经过x轴上两点A,B,点B的坐标为(3,0),与y轴相交于点C.
(1)求抛物线的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)在平面直角坐标系中,点P(x0,y0)到直线Ax+By+C=0的距离公式是![]()
如:求点P(1,2)到直线y=﹣![]() x+1的距离d
x+1的距离d
解:将直线解析式变形为4x+3y﹣3=0,则A=4,B=3,C=﹣3
所以![]()
(解决问题)已知直线l1的解析式是y=-![]() x+1
x+1
(1)若点P的坐标为(1,﹣2),则点P到直线l1的距离是 ;
(2)若直线l2与直线l1平行,且两条平行线间的距离是![]() ,请求出直线l2的解析式.
,请求出直线l2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
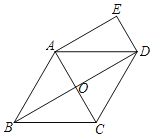
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=2,∠BCD=120°,求四边形AODE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴的两个交点是点
轴的两个交点是点![]() ,
,![]() (
(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴的交点是点
轴的交点是点![]() .
.
(1)求证:![]() ,
,![]() 两点中必有一个点坐标是
两点中必有一个点坐标是![]() ;
;
(2)若抛物线的对称轴是![]() ,求其解析式;
,求其解析式;
(3)在(2)的条件下,抛物线上是否存在一点![]() ,使
,使![]() ?如果存在,求出点
?如果存在,求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网瘾低龄化已引起社会各界的高度关注,有关部门在全国范围内对12~35岁的网瘾人群进行了随机抽样查,得到了如下两个不定整的统计图,请根据图中信息解答下列问题:
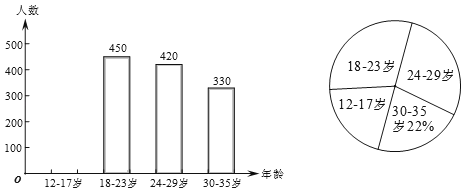
(1)求本次调查了多少名网瘾人员?
(2)通过计算补全条形统计图,在扇形统计图中,18~23岁部分的圆心角的度数为 ;
(3)目前我国12﹣35岁网瘾人数约为3000万,请估计其中12﹣23岁的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(m﹣2)x﹣![]() =0.
=0.
(1)求证:无论m为何值,方程总有两个不相等实数根.
(2)设方程的两实数根为x1,x2,且满足(x1+x2)2=|x1|﹣|x2|+2,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,将点A向右平移6个单位长度,得到点B.
,将点A向右平移6个单位长度,得到点B.
(1)直接写出点B的坐标;
(2)若抛物线y=-x2+bx+c经过点A,B,求抛物线的表达式;
(3)若抛物线y=-x2+bx+c的顶点在直线y=x+2上移动,当抛物线与线段AB有且只有一个公共点时,求抛物线顶点横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com