练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知在平面直角坐标系内，抛物线y＝x2﹣bx+6经过x轴上两点A，B，点B的坐标为（3，0），与y轴相交于点C．

    （1）求抛物线的解析式；

    （2）求△ABC的面积．

    【答案】（1）y＝x2﹣5x+6；（2）3

    【解析】

    （1）把点B的坐标（3，0）代入抛物线y＝x2﹣bx+6，即可得出抛物线的表达式y＝x2﹣5x+6；

    （2）先求出A（2，0），B（3，0），C（0，6），再利用三角形面积公式求解即可．

    解：（1）把点B的坐标（3，0）代入抛物线y＝x2﹣bx+6，得0＝9﹣3b+6，

    解得：b＝5，

    ∴抛物线的表达式y＝x2﹣5x+6；

    （2）∵抛物线的表达式y＝x2﹣5x+6；

    令y=0，则x2﹣5x+6=0，

    解得：x1=2，x2=3；

    ∴A（2，0），B（3，0），C（0，6），

    ∴S△ABC＝×1×6＝3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】对于平面直角坐标系xOy中的点P和⊙C，给出如下定义：若⊙C上存在一个点M，使得PM = MC，则称点P为⊙C的“等径点”．已知点D，E，F．

    （1）当⊙O的半径为1时，

    ①在点D，E，F中，⊙O的“等径点”是 ；

    ②作直线EF，若直线EF上的点T（m，n）是⊙O的“等径点”，求m的取值范围．

    （2）过点E作EG⊥EF交x轴于点G，若△EFG上的所有点都是某个圆的“等径点”，求这个圆的半径r的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线与轴，轴分别交于点，经过点的抛物线与轴的另一个交点为点，点是抛物线上一点，过点作轴于点，连接，设点的横坐标为.

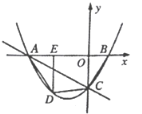
    求抛物线的解析式；

    当点在第三象限，设的面积为，求与的函数关系式，并求出的最大值及此时点的坐标；

    连接，若,请直接写出此时点的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

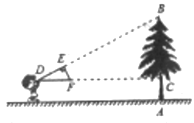
    【题目】如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上，已知纸板的两条直角边DE=0.4m，EF=0.2m，测得边DF离地面的高度AC=1.5m，CD=8m，求树高。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某驻村扶贫小组实施产业扶贫，帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元/千克，规定销售单价不低于成本，又不高于成本的两倍.经过市场调查发现，某天西瓜的销售量y(千克)与销售单价x(元/千克)的函数关系如下图所示：

    (1)求y与x的函数解析式(也称关系式)；

    (2)求这一天销售西瓜获得的利润的最大值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

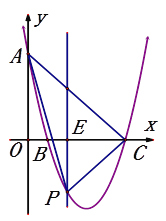
    【题目】在平面直角坐标系中，抛物线与y轴的交点为A，与x轴的正半轴分别交于点B（b，0），C（c，0）.

    （1）当b=1时，求抛物线相应的函数表达式；

    （2）当b=1时，如图，E（t，0）是线段BC上的一动点,过点E作平行于y轴的直线l与抛物线的交点为P．求△APC面积的最大值；

    （3）当c =b+ n.时，且n为正整数.线段BC（包括端点）上有且只有五个点的横坐标是整数，求b的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

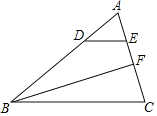
    【题目】如图，在△ABC中，BC＝9，∠ABC的平分线BF交AC于点F，点D、点E分别是边AB、AC上的点，若，则BD﹣DE的值为（　　）

    A.3B.3．5C.4D.4．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1），二次函数y＝ax2﹣bx（a≠0）的图象与x轴、直线y＝x的交点分别为点A(4，0)、B(5，5)．

    （1）a＝　 　，b＝　 　，∠AOB＝　 　°；

    （2）连接AB，点P是抛物线上一点（异于点A），且∠PBO＝∠OBA，求点P的坐标　 　；

    （3）如图（2），点C、D是线段OB上的动点，且CD＝2．设点C的横坐标为m．

    ①过点C、D分别作x轴的垂线，与抛物线相交于点F、E，连接EF．当CF+DE取得最大值时，求m的值并判断四边形CDEF的形状；

    ②连接AC、AD，求m为何值时，AC+AD取得最小值，并求出这个最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店经营家居收纳盒，已知成批购进时的单价是20元．调查发现：销售单价是30元时，月销售量是230件，而销售单价每上涨1元，月销售量就减少10件，但每个收纳盒售价不能高于40元．设每个收纳盒的销售单价上涨了元时（为正整数），月销售利润为元．

    （1）求与的函数关系式．

    （2）每个收纳盒的售价定为多少元时，月销售利润恰为2520元？

    （3）每件玩具的售价定为多少元时可使月销售利润最大？最大的月利润是多少？

    查看答案和解析>>

    同步练习册答案