
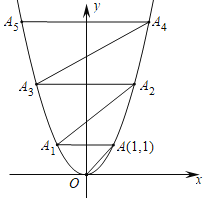
【题目】在平面直角坐标系中,抛物线y=x2如图所示,已知A点坐标为(1,1),过点A作AA1∥x轴交抛物线于点A1,过点A1作A1A2∥OA交抛物线于点A2,过点A2作A2A3∥x轴交抛物线于点A3,过点A3作A3A4∥OA交抛物线于点A4,过点A4作A4A5∥x轴交抛物线于点A5,则点A5的坐标为_____.
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.
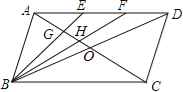
(1)求EG:BG的值;
(2)求证:AG=OG;
(3)设AG=a,GH=b,HO=c,求a:b:c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在一个点M,使得PM = MC,则称点P为⊙C的“等径点”.已知点D![]() ,E
,E![]() ,F
,F![]() .
.
(1)当⊙O的半径为1时,
①在点D,E,F中,⊙O的“等径点”是 ;
②作直线EF,若直线EF上的点T(m,n)是⊙O的“等径点”,求m的取值范围.
(2)过点E作EG⊥EF交x轴于点G,若△EFG上的所有点都是某个圆的“等径点”,求这个圆的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝中华人民共和国成立70周年,某市决定开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了下列不完整的统计图表.
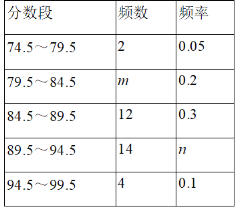
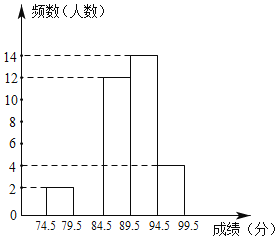
(1)表中m= ,n= ;
(2)请在图中补全频数直方图;
(3)甲同学的比赛成绩是40位参赛选手成绩的中位数,据此推测他的成绩落在 分数段内;
(4)选拔赛中,成绩在94.5分以上的选手,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列举法或树状图法求恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖户长期承包一口鱼糖养鱼,每年养殖一批,从鱼苗放入养到成品需要300天,鱼糖承包费用每年5000元,他记录了前几年平均每天投入饲料量(单位:kg)与年底成品鱼(达到一定规格可以销售)产量之间的关系如下表:
平均每天投入饲料(kg) | 20 | 25 | 30 | 40 | 50 | 60 | 70 | 80 |
成品鱼产量(kg) | 2800 | 3000 | 3200 | 3600 | 3900 | 4000 | 3900 | 3600 |
(1)请用适当的函数模型描述平均每天投入饲料数量与成品鱼产量之间的关系;
(2)如果今年的饲料价格为1.6元/kg,成品鱼销售价为20元/kg,鱼苗费用4000元,假设养成的成品鱼全部都能按此价格卖出.请建立适当的函数模型平均每天投入饲料多少千克时,该养殖户当年在该鱼糖养殖这种鱼获得的利润最多,最多利润是多少元?(利润=销售收入﹣饲料成本﹣鱼糖承包费﹣鱼苗成本).
查看答案和解析>>
科目:初中数学 来源: 题型:
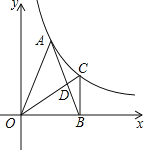
【题目】如图,A为反比例函数y=![]() (其中x>0)图象上的一点,在x轴正半轴上有一点B,OB=4.连接OA、AB,且OA=AB=2
(其中x>0)图象上的一点,在x轴正半轴上有一点B,OB=4.连接OA、AB,且OA=AB=2![]() .
.
(1)求k的值;
(2)过点B作BC⊥OB,交反比例函数y=![]() (x>0)的图象于点C.
(x>0)的图象于点C.
①连接AC,求△ABC的面积;
②在图上连接OC交AB于点D,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,经过点
,经过点![]() 的抛物线
的抛物线![]() 与
与![]() 轴的另一个交点为点
轴的另一个交点为点![]() ,点
,点![]() 是抛物线上一点,过点
是抛物线上一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 当点
当点![]() 在第三象限,设
在第三象限,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值及此时点
的最大值及此时点![]() 的坐标;
的坐标;
![]() 连接
连接![]() ,若
,若![]() ,请直接写出此时点
,请直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
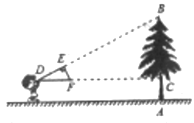
【题目】如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=0.4m,EF=0.2m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高。
查看答案和解析>>
科目:初中数学 来源: 题型:
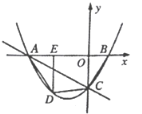
【题目】如图(1),二次函数y=ax2﹣bx(a≠0)的图象与x轴、直线y=x的交点分别为点A(4,0)、B(5,5).

(1)a= ,b= ,∠AOB= °;
(2)连接AB,点P是抛物线上一点(异于点A),且∠PBO=∠OBA,求点P的坐标 ;
(3)如图(2),点C、D是线段OB上的动点,且CD=2![]() .设点C的横坐标为m.
.设点C的横坐标为m.
①过点C、D分别作x轴的垂线,与抛物线相交于点F、E,连接EF.当CF+DE取得最大值时,求m的值并判断四边形CDEF的形状;
②连接AC、AD,求m为何值时,AC+AD取得最小值,并求出这个最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com