
【题目】如图,在ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.
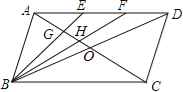
(1)求EG:BG的值;
(2)求证:AG=OG;
(3)设AG=a,GH=b,HO=c,求a:b:c的值.
【答案】(1)1:3;(2)见解析;(3)5:3:2.
【解析】
(1)根据平行四边形的性质可得AO=![]() AC,AD=BC,AD∥BC,从而可得△AEG∽△CBG,由AE=EF=FD可得BC=3AE,然后根据相似三角形的性质,即可求出EG:BG的值;
AC,AD=BC,AD∥BC,从而可得△AEG∽△CBG,由AE=EF=FD可得BC=3AE,然后根据相似三角形的性质,即可求出EG:BG的值;
(2)根据相似三角形的性质可得GC=3AG,则有AC=4AG,从而可得AO=![]() AC=2AG,即可得到GO=AO﹣AG=AG;
AC=2AG,即可得到GO=AO﹣AG=AG;
(3)根据相似三角形的性质可得AG=![]() AC,AH=
AC,AH=![]() AC,结合AO=
AC,结合AO=![]() AC,即可得到a=
AC,即可得到a=![]() AC,b=
AC,b=![]() AC,c=
AC,c=![]() AC,就可得到a:b:c的值.
AC,就可得到a:b:c的值.
(1)∵四边形ABCD是平行四边形,
∴AO=![]() AC,AD=BC,AD∥BC,
AC,AD=BC,AD∥BC,
∴△AEG∽△CBG,
∴![]() .
.
∵AE=EF=FD,
∴BC=AD=3AE,
∴GC=3AG,GB=3EG,
∴EG:BG=1:3;
(2)∵GC=3AG(已证),
∴AC=4AG,
∴AO=![]() AC=2AG,
AC=2AG,
∴GO=AO﹣AG=AG;
(3)∵AE=EF=FD,
∴BC=AD=3AE,AF=2AE.
∵AD∥BC,
∴△AFH∽△CBH,
∴![]() ,
,
∴![]() =
=![]() ,即AH=
,即AH=![]() AC.
AC.
∵AC=4AG,
∴a=AG=![]() AC,
AC,
b=AH﹣AG=![]() AC﹣
AC﹣![]() AC=
AC=![]() AC,
AC,
c=AO﹣AH=![]() AC﹣
AC﹣![]() AC=
AC=![]() AC,
AC,
∴a:b:c=![]() :
:![]() :
:![]() =5:3:2.
=5:3:2.


科目:初中数学 来源: 题型:
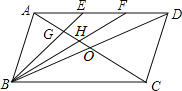
【题目】为了了解某校初中各年级学生每天的平均睡眠时间(单位:h,精确到1h),抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数a的值为 ,所抽查的学生人数为 .
(2)求出平均睡眠时间为8小时的人数,并补全频数直方图.
(3)求出这部分学生的平均睡眠时间的众数和平均数.
(4)如果该校共有学生1200名,请你估计睡眠不足(少于8小时)的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )

A. abc<0 B. -3a+c<0
C. b2-4ac≥0 D. 将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c
查看答案和解析>>
科目:初中数学 来源: 题型:
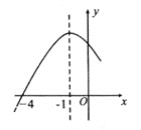
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-4,0),对称轴为直线x=-1,下列结论:
①abc>0;
②2a-b=0;
③一元二次方程ax2+bx+c=0的解是x1=-4,x2=1;
④当y>0时,-4<x<2.
其中正确的结论有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求二次函数![]() 的图象如图所示,其对称轴为直线
的图象如图所示,其对称轴为直线![]() ,与
,与![]() 轴的交点为
轴的交点为![]() 、
、![]() ,其中
,其中![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;其中,正确的结论有( )
;其中,正确的结论有( )
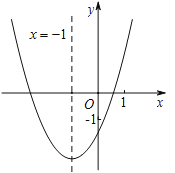
A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺指针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…,若点A(![]() ,0)、B(0,4),则点B2020的横坐标为_____.
,0)、B(0,4),则点B2020的横坐标为_____.
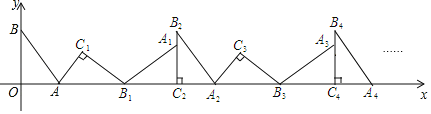
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=x2如图所示,已知A点坐标为(1,1),过点A作AA1∥x轴交抛物线于点A1,过点A1作A1A2∥OA交抛物线于点A2,过点A2作A2A3∥x轴交抛物线于点A3,过点A3作A3A4∥OA交抛物线于点A4,过点A4作A4A5∥x轴交抛物线于点A5,则点A5的坐标为_____.
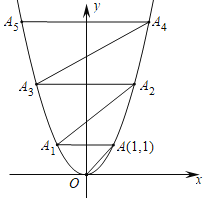
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com