
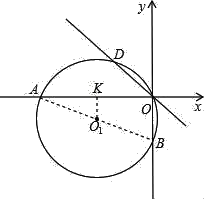
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�У���D��ֱ��y=��x��һ�㣬��O��D�����Բ��O1�ֱ�x�ᡢy���ڵ�A��B��
��1����A����12��0����B��0����5��ʱ����O1�����ꣻ

��2���ڣ�1���������£�����A����O1��������BD���ӳ����ཻ�ڵ�C�����C�����ꣻ

��3������D�ĺ�����Ϊ![]() ����IΪ��ABO�����ģ�IE��AB��E������O��D����ġ�O1�Ĵ�С�����仯ʱ������ۣ�AE��BE��ֵ�Ƿ����仯�������䣬�������ֵ�����仯��������仯��Χ��
����IΪ��ABO�����ģ�IE��AB��E������O��D����ġ�O1�Ĵ�С�����仯ʱ������ۣ�AE��BE��ֵ�Ƿ����仯�������䣬�������ֵ�����仯��������仯��Χ��

���𰸡���1��O1����6����2.5������2��C����7��12������3��������.
��������
��1������AB������O1��O1K��OA�ڵ�K���ɡ�AOB=90������֪��AB��Բ��O1����֪��A����B�����꣬O1A=O1B����O1K=![]() OB��OK=
OB��OK=![]() OA���Ӷ��ɽ���O1�����������
OA���Ӷ��ɽ���O1�����������
��2��֤��ACH�ա�BAO����CH=OA��OH=AO-OB���Ӷ��ɽ���C�����������
��3���������ߣ���DN��X����N��DM��Y����M����֪���ı���DMONΪ�����Σ�ͨ��֤����ADN�ա�BDM����AN=BM����AE-BEAG-BF=��OA-OG��-��OB-OF��=OA-OB=��AN+OG��-��AN-MO��=OG+OM=7Ϊ��ֵ��
��1������AB������O1��O1K��OA�ڵ�K��
�ߡ�AOB=90�㣬
��AB����Բ��O1��
��A����12��0����B��0����5����O1K��O1A��O1A=O1B��
��O1K=![]() OB=2.5��OK=
OB=2.5��OK=![]() OA=
OA=![]() ��12=6��
��12=6��
��O1����6����2.5����
��2������C��CH��x���ڵ�H������AD��AB��

��AC��O1������
���CAB=90�㣬
��ֱ��OD����ʽΪy=��x��
���AOD=��ABD=45�㣬
���ABCΪ����ֱ�������Σ�
��AC=AB��
��ACΪ��O1�����ߣ�
���CAH=��ABO��
�ߡ�CHA=��AOB=90�㣬AC=AB��
���ACH�ա�BAO��
��CH=OA=12��OH=AO��OB=12��5=7��
���C����7��12����
��3��D��ֱ��y=��x��һ�㣬��DN��X����N��DM��Y����M��

DM=DN=NO=MO��G��F�ֱ�����X�ᡢY����е㣬��AE=AG��BE=BF��IG=OG=OF=IF��
�ߡ�ADN+��NDB=90�㣬��BDM+��NDB=90��
���ADN=��BDM��
�ߡ�ADN=��BDM��ND=DM����AND=��BMD=90��
���ADN�ա�BDM��
��AN=BM��
��AE��BE=AG��BF��=��OA��OG������OB��OF��=OA��OB=��AN+ON������AN��MO��=ON+OM=![]() =7��
=7��


 ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
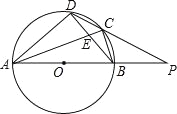
����Ŀ����ͼ���ı���ABCD�ڽ��ڡ�O��AB�ǡ�O��ֱ����AC��BD�ཻ�ڵ�E����DC2=CECA��
��1����֤��BC=CD��
��2���ֱ��ӳ�AB��DC���ڵ�P����PB=OB��CD=2![]() �����O�İ뾶��
�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ����ֽ��С�����εı߳�Ϊ1��
����ֽ��С�����εı߳�Ϊ1��![]() ��
��![]() �����ڸ���ϣ�Ҫ��ͼ�и�����ҵ���
�����ڸ���ϣ�Ҫ��ͼ�и�����ҵ���![]() ��ʹ��
��ʹ��![]() �����Ϊ2�����������ĵ�
�����Ϊ2�����������ĵ�![]() �У� ��
�� ��

A.������B.7��C.6��D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵ���![]() �͵���
�͵���![]() �У�
��![]() ��
��![]() ������
������![]() ���ڵ�
���ڵ�![]() .
.
(1����ͼ1����![]() ��
��
��![]() ��
��![]() ��������ϵΪ ��
��������ϵΪ ��
��![]() �Ķ���Ϊ ��
�Ķ���Ϊ ��
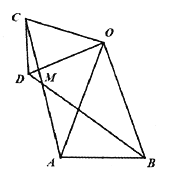
ͼ1
��2����ͼ2����![]() ��
��
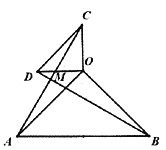
ͼ2
���ж�![]() ��
��![]() ֮�����������������ϵ����˵�����ɣ�
֮�����������������ϵ����˵�����ɣ�
����![]() �Ķ�����
�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
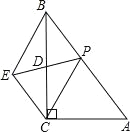
����Ŀ����ͼ���ڡ�ABC�У���ACB=90�㣬AC=15��sin��A=![]() ����D��BC���е㣬��P��AB��һ���㣨�����B�غϣ����ӳ�PD��E��ʹDE=PD������EB��EC��
����D��BC���е㣬��P��AB��һ���㣨�����B�غϣ����ӳ�PD��E��ʹDE=PD������EB��EC��
��1����֤���ı���PBEC��ƽ���ı��Σ�
��2����գ�
�ٵ�AP��ֵΪ�� ��ʱ���ı���PBEC�Ǿ��Σ�
�ڵ�AP��ֵΪ�� ��ʱ���ı���PBEC�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
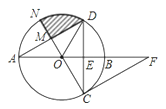
����Ŀ����ͼ��ABΪ��O��ֱ������CD��ֱƽ��OB�ڵ�E����F��AB�ӳ����ϣ���AFC=30����
��1����֤��CFΪ��O�����ߣ�
��2�����뾶ON��AD�ڵ�M��CE=![]() ����ͼ����Ӱ���ֵ������
����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
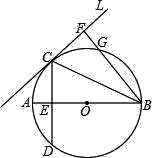
����Ŀ����ͼ����֪AB�ǡ�O��ֱ����ֱ��l���O�����ڵ�C��![]() ����CD��AB��E��BF��l������ΪF��BF����O��G��
����CD��AB��E��BF��l������ΪF��BF����O��G��
��1����֤��CE2=FGFB��
��2����tan��CBF=![]() ��AE=3�����O��ֱ����
��AE=3�����O��ֱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
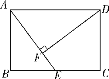
����Ŀ����ͼ���ھ���ABCD�У�E��BC�ߵ��е㣬DF��AE������ΪF.
(1)��֤����ADF�ס�EAB��
(2)��AB��4��AD��6����DF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ���Ӧ�ã�
�Ķ�1��a��bΪʵ������a��0��b��0����Ϊ![]() ������
������![]() ���Ӷ�
���Ӷ�![]() ����a��bʱȡ�Ⱥţ���
����a��bʱȡ�Ⱥţ���
�Ķ�2������![]() ������m��0��x��0�������Ķ�1���ۿ�֪��
������m��0��x��0�������Ķ�1���ۿ�֪�� ![]()
![]() �����Ե�
�����Ե�![]() ��
��![]() ʱ������
ʱ������![]() ����СֵΪ
����СֵΪ![]() ��
��
�Ķ������������ݣ�����������⣺
����1����֪һ�����ε����Ϊ4������һ�߳�Ϊx������һ�߳�Ϊ![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() ����x��__________ʱ���ܳ�����СֵΪ__________��
����x��__________ʱ���ܳ�����СֵΪ__________��
����2����֪����y1��x��1��x����1���뺯��y2��x2��2x��17��x����1������x��__________ʱ�� ![]() ����СֵΪ__________��
����СֵΪ__________��
����3��ij���ѧϰÿ���֧���ܷ��ð��������������֣�һ�ǽ�ְ������6400Ԫ������ѧ�������ÿ��10Ԫ�������������ã����У�����������ѧ��������ƽ�������ȣ�����ϵ��Ϊ0.01����ѧУѧ������Ϊ����ʱ����Уÿ������Ͷ����ͣ���ͷ����Ƕ���Ԫ��������Ͷ�룽֧���ܷ��á�ѧ��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com