
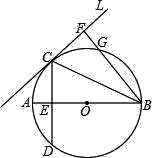
【题目】如图,已知AB是⊙O的直径,直线l与⊙O相切于点C且![]() ,弦CD交AB于E,BF⊥l,垂足为F,BF交⊙O于G.
,弦CD交AB于E,BF⊥l,垂足为F,BF交⊙O于G.
(1)求证:CE2=FGFB;
(2)若tan∠CBF=![]() ,AE=3,求⊙O的直径.
,AE=3,求⊙O的直径.
【答案】(1)见解析;(2)15.
【解析】
(1)由切割线定理知:CF2=FGFB,欲证本题的结论,需先证得CE=CF;可通过证△BCE≌△BCF得出;
(2)欲求⊙O的直径,已知AE的长,关键是求出BE的长度;在Rt△ABC中,CE⊥AB,根据射影定理得到CE2=AEEB,由此可求出BE的长.
(1)连接AC,
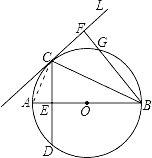
∵AB为直径,
∴∠ACB=90°,
∵![]() ,且AB是直径,
,且AB是直径,
∴AB⊥CD,
即CE是Rt△ABC的高,
∴∠A=∠ECB,∠ACE=∠EBC,
∵CF是⊙O的切线,
∴∠FCB=∠A,CF2=FGFB,
∴∠FCB=∠ECB,
∵∠BFC=∠CEB=90°,CB=CB,
∴△BCF≌△BCE,
∴CE=CF,∠FBC=∠CBE,
∴CE2=FGFB;
(2)∵∠CBF=∠CBE,∠CBE=∠ACE,
∴∠ACE=∠CBF;
∴tan∠CBF=tan∠ACE=![]() ,
,
∵AE=3,
∴![]() ,
,
∴CE=6,
在Rt△ABC中,CE是高,
∴CE2=AEEB,即62=3EB,
∴EB=12,
∴⊙O的直径为:12+3=15.


科目:初中数学 来源: 题型:
【题目】我们知道,经过原点的抛物线可以用y=ax2+bx(a≠0)表示,对于这样的抛物线:
(1)当抛物线经过点(﹣2,0)和(﹣1,3)时,求抛物线的表达式;
(2)当抛物线的顶点在直线y=﹣2x上时,求b的值;
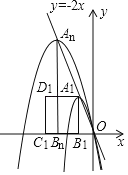
(3)如图,现有一组这样的抛物线,它们的顶点A1、A2、…,An在直线y=﹣2x上,横坐标依次为﹣1,﹣2,﹣3,…,﹣n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1、B2,…,Bn,以线段AnBn为边向左作正方形AnBnCnDn,如果这组抛物线中的某一条经过点Dn,求此时满足条件的正方形AnBnCnDn的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买![]() 种图书花费了3000元,购买
种图书花费了3000元,购买![]() 种图书花费了1600元,A种图书的单价是
种图书花费了1600元,A种图书的单价是![]() 种图书的1.5倍,购买
种图书的1.5倍,购买![]() 种图书的数量比
种图书的数量比![]() 种图书多20本.
种图书多20本.
(1)求![]() 和
和![]() 两种图书的单价;
两种图书的单价;
(2)书店在“世界读书日”进行打折促销活动,所有图书都按8折销售学校当天购买了![]() 种图书20本和
种图书20本和![]() 种图书25本,共花费多少元?
种图书25本,共花费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:在平面直角坐标系中,点D是直线y=﹣x上一点,过O、D两点的圆⊙O1分别交x轴、y轴于点A和B.
(1)当A(﹣12,0),B(0,﹣5)时,求O1的坐标;

(2)在(1)的条件下,过点A作⊙O1的切线与BD的延长线相交于点C,求点C的坐标;

(3)若点D的横坐标为![]() ,点I为△ABO的内心,IE⊥AB于E,当过O、D两点的⊙O1的大小发生变化时,其结论:AE﹣BE的值是否发生变化?若不变,请求出其值;若变化,请求出变化范围.
,点I为△ABO的内心,IE⊥AB于E,当过O、D两点的⊙O1的大小发生变化时,其结论:AE﹣BE的值是否发生变化?若不变,请求出其值;若变化,请求出变化范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
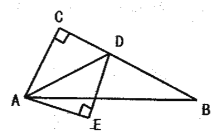
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的动点,连接
边上的动点,连接![]() ,以
,以![]() 为斜边在
为斜边在![]() 的下方作等腰直角三角形
的下方作等腰直角三角形![]() .
.
(1)填空:![]() 的面积等于 ;
的面积等于 ;
(2)连接![]() ,求证:
,求证:![]() 是
是![]() 的平分线;
的平分线;
(3)点![]() 在
在![]() 边上,且
边上,且![]() , 当
, 当![]() 从点
从点![]() 出发运动至点
出发运动至点![]() 停止时,求点
停止时,求点![]() 相应的运动路程.
相应的运动路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.
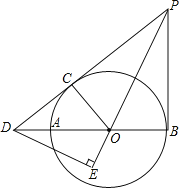
(1)求证:PB是的切线.
(2)若PB=6,DB=8,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
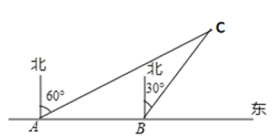
【题目】为了维护国家主权和海洋权力,海监部门对我国领海实行常态化巡航管理,如图,正在执行巡航任务的海监船以每小时30海里的速度向正东方航行,在![]() 处测得灯塔
处测得灯塔![]() 在北偏东60°方向上, 继续航行
在北偏东60°方向上, 继续航行![]() 后到达
后到达![]() 处, 此时测得灯塔
处, 此时测得灯塔![]() 在北偏东30°方向上.
在北偏东30°方向上.
(1) 求![]() 的度数;
的度数;
(2)已知在灯塔![]() 的周围15海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围15海里内有暗礁,问海监船继续向正东方向航行是否安全?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com