
【题目】我们知道,经过原点的抛物线可以用y=ax2+bx(a≠0)表示,对于这样的抛物线:
(1)当抛物线经过点(﹣2,0)和(﹣1,3)时,求抛物线的表达式;
(2)当抛物线的顶点在直线y=﹣2x上时,求b的值;
(3)如图,现有一组这样的抛物线,它们的顶点A1、A2、…,An在直线y=﹣2x上,横坐标依次为﹣1,﹣2,﹣3,…,﹣n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1、B2,…,Bn,以线段AnBn为边向左作正方形AnBnCnDn,如果这组抛物线中的某一条经过点Dn,求此时满足条件的正方形AnBnCnDn的边长.
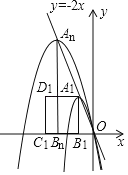
【答案】(1)抛物线的表达式为y=﹣3x2﹣6x;(2)b1=﹣4,b2=0;(3)正方形的边长是10.
【解析】试题分析:(1)把点(﹣2,0)和(﹣1,3)分别代入y=ax2+bx,得到关于a、b的二元一次方程组,解方程组即可;
(2)根据二次函数的性质,得出抛物线y=ax2+bx的顶点坐标是(﹣![]() ,﹣
,﹣![]() ),把顶点坐标代入y=﹣2x,得出﹣
),把顶点坐标代入y=﹣2x,得出﹣![]() =﹣2×(﹣
=﹣2×(﹣![]() ),即可求出b的值;
),即可求出b的值;
(3)由于这组抛物线的顶点A1、A2、…,An在直线y=﹣2x上,根据(2)的结论可知,b=4或b=0.①当b=0时,不合题意舍去;②当b=﹣4时,抛物线的表达式为y=ax2﹣4x.由题意可知,第n条抛物线的顶点为An(﹣n,2n),则Dn(﹣3n,2n),因为以An为顶点的抛物线不可能经过点Dn,设第n+k(k为正整数)条抛物线经过点Dn,此时第n+k条抛物线的顶点坐标是An+k(﹣n﹣k,2n+2k),根据﹣![]() =﹣n﹣k,得出a=
=﹣n﹣k,得出a=![]() =﹣
=﹣![]() ,即第n+k条抛物线的表达式为y=﹣
,即第n+k条抛物线的表达式为y=﹣![]() x2﹣4x,根据Dn(﹣3n,2n)在第n+k条抛物线上,得到2n=﹣
x2﹣4x,根据Dn(﹣3n,2n)在第n+k条抛物线上,得到2n=﹣![]() ×(﹣3n)2﹣4×(﹣3n),解得k=
×(﹣3n)2﹣4×(﹣3n),解得k=![]() n,进而求解即可.
n,进而求解即可.
试题解析:(1)∵抛物线y=ax2+bx经过点(﹣2,0)和(﹣1,3),
∴![]() ,解得
,解得![]() ,
,
∴抛物线的表达式为y=﹣3x2﹣6x;
(2)∵抛物线y=ax2+bx的顶点坐标是(﹣![]() ,﹣
,﹣![]() ),且该点在直线y=﹣2x上,
),且该点在直线y=﹣2x上,
∴﹣![]() =﹣2×(﹣
=﹣2×(﹣![]() ),
),
∵a≠0,∴﹣b2=4b,
解得b1=﹣4,b2=0;
(3)这组抛物线的顶点A1、A2、…,An在直线y=﹣2x上,
由(2)可知,b=4或b=0.
①当b=0时,抛物线的顶点在坐标原点,不合题意,舍去;
②当b=﹣4时,抛物线的表达式为y=ax2﹣4x.
由题意可知,第n条抛物线的顶点为An(﹣n,2n),则Dn(﹣3n,2n),
∵以An为顶点的抛物线不可能经过点Dn,设第n+k(k为正整数)条抛物线经过点Dn,此时第n+k条抛物线的顶点坐标是An+k(﹣n﹣k,2n+2k),
∴﹣![]() =﹣n﹣k,∴a=
=﹣n﹣k,∴a=![]() =﹣
=﹣![]() ,
,
∴第n+k条抛物线的表达式为y=﹣![]() x2﹣4x,
x2﹣4x,
∵Dn(﹣3n,2n)在第n+k条抛物线上,
∴2n=﹣![]() ×(﹣3n)2﹣4×(﹣3n),解得k=
×(﹣3n)2﹣4×(﹣3n),解得k=![]() n,
n,
∵n,k为正整数,且n≤12,
∴n1=5,n2=10.
当n=5时,k=4,n+k=9;
当n=10时,k=8,n+k=18>12(舍去),
∴D5(﹣15,10),
∴正方形的边长是10.


科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题
数学课上,同学们兴致勃勃地探讨着利用不同画图工具画角的平分线的方法.
小惠说:“如图1,我用相同的两块含 30°角的直角三角板可以画角的平分线.画法如下:
①在 ![]() 的两边分别取点 M,N,使 OM=ON ;
的两边分别取点 M,N,使 OM=ON ;
②把直角三角板按如图所示的位置放置,两斜边交于点 P ;
③作射线 OP .则OP是∠AOB 的平分线.”小旭说:“我只用刻度尺就可以画角平分线.”
请你也参与探讨,解决以下问题:
(1)小惠的作法正确吗?若正确,请给出证明,若不正确,请说明理由.
(2)请你和小旭一样,只用刻度尺画出图 2 中∠QRS 的平分线,并简述画图的过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
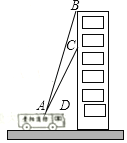
【题目】贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“知识改变命运,科技繁荣祖国”,我市中小学每年都要举办一届科技运动会,下图为我市某校今年参加科技运动会航模比赛(包括空模、海模、车模、建模四个类别)的参赛人数统计图:

(1)该校参加车模、建模比赛的人数分别是 人和 人:
(2)该校参加航模比赛的总人数是 人,空模所在扇形的圆心角的度数是 ,并把条形统计图补充完整.
(3)从全市中小学参加航模比赛选手中随机抽取80人,其中有32人获奖,今年我市中小学参加航模比赛人共有2485人,请你估算今年参加航模比赛的获奖人数约是多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com