
某园艺公司对一块直角三角形的花园进行改造,测得两直角边长分别为a=6米,b=8米.现要将其扩建成等腰三角形,且扩充部分是以b为直角边的直角三角形,则扩建后的等腰三角形花圃的周长为( )米.
A.32或20+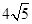
B.32或36或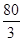
C.32或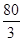 或20+
或20+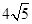
D.32或36或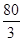 或20+
或20+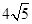
C
【解析】由于扩充所得的等腰三角形腰和底不确定,若设扩充所得的三角形是△ABD,则应分为①AB=AD,②AD=BD两种情况进行讨论.
【解析】
如图所示:在Rt△ABC中,
∵AC=8m,BC=6m,
∴AB=10m,

如图1,当AB=AD时,CD=BC=6m,
此时等腰三角形花圃的周长=10+10+6+6=32(m);
如图2:当AD=BD时,设AD=BD=xm;
Rt△ACD中,BD=xm,CD=(x﹣6)m;
由勾股定理,得AD2=DC2+CA2,即(x﹣6)2+82=x2,解得x=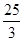 ;
;
此时等腰三角形绿地的周长=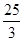 ×2+10=
×2+10=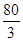 (m).
(m).
当AB=BD时,在Rt△ACD中,AD=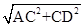 =
=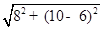 =
=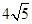 ,
,
∴等腰三角形绿地的周长=2×10+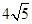 =20+
=20+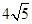 .
.
故选C.


科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:填空题
如图(a),有一张矩形纸片ABCD,其中AD=6cm,以AD为直径的半圆,正好与对边BC相切,将矩形纸片ABCD沿DE折叠,使点A落在BC上,如图(b).则半圆还露在外面的部分(阴影部分)的面积为 .

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的对称、平移与旋转(解析版) 题型:选择题
如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3, ),点C的坐标为(
),点C的坐标为( ,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )

A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学反比例函数(解析版) 题型:解答题
平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A(-4,0),B(2,0),C(3,3),反比例函数y=  的图象经过点C.
的图象经过点C.

(1)求此反比例函数的解析式;
(2)将平行四边形ABCD沿x轴翻折得到平行四边形AD′C′B,请你通过计算说明点D′在双曲线上;
(3)请你画出△AD′C,并求出它的面积.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学函数基础知识(解析版) 题型:选择题
梅凯种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如图所示,下列四种说法:
①一次购买种子数量不超过10千克时,销售价格为5元/千克;
②一次购买30千克种子时,付款金额为100元;
③一次购买10千克以上种子时,超过10千克的那部分种子的价格打五折;
④一次购买40千克种子比分两次购买且每次购买20千克种子少花25元钱.
其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学二次函数综合应用(解析版) 题型:解答题
如图1,已知正方形ABCD的边长为1,点E在边BC上,若∠AEF=90°,且EF交正方形外角的平分线CF于点F.
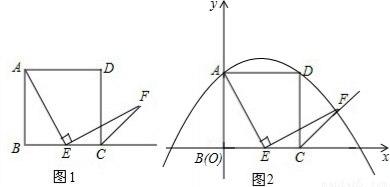
(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);
(2)如图2,若点E在线段BC上滑动(不与点B,C重合).
①AE=EF是否总成立?请给出证明;
②在如图2的直角坐标系中,当点E滑动到某处时,点F恰好落在抛物线y=-x2+x+1上,求此时点F的坐标.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学三角形(一)(解析版) 题型:选择题
如图,BO、CO分别平分∠ABC与∠ACB,MN∥BC,若AB=36,AC=24,则△AMN的周长是( )
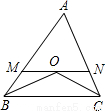
A.60 B.66 C.72 D.78
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com