
平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A(-4,0),B(2,0),C(3,3),反比例函数y=  的图象经过点C.
的图象经过点C.

(1)求此反比例函数的解析式;
(2)将平行四边形ABCD沿x轴翻折得到平行四边形AD′C′B,请你通过计算说明点D′在双曲线上;
(3)请你画出△AD′C,并求出它的面积.
(1)y=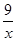 (2)见解析 (3)12,图形见解析
(2)见解析 (3)12,图形见解析
【解析】(1)把点C(3,3)代入反比例函数y= 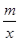 ,求出m,即可求出解析式;
,求出m,即可求出解析式;
(2)过C作CE⊥x轴于点E,过D作DF⊥x轴于点F,则△CBE≌△DAF,根据线段之间的数量关系进一步求出点D的坐标,再点D′与点D关于x轴对称,求出D′坐标,进而判断点D′是不是在双曲线;
(3)根据C(3,3),D′(-3,-3)得到点C和点D′关于原点O中心对称,进一步得出D′O=CO= 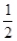 D′C,由S△AD′C=2S△AOC=2×
D′C,由S△AD′C=2S△AOC=2×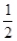 AO•CE求出面积的值.
AO•CE求出面积的值.
【解析】
(1)∵点C(3,3)在反比例函数y=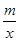 的图象上,
的图象上,
∴3=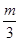 ,
,
∴m=9,
∴反比例函数的解析式为y=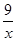 ;
;
(2)过C作CE⊥x轴于点E,过D作DF⊥x轴于点F,则△CBE≌△DAF,
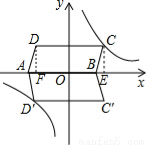
∴AF=BE,DF=CE,
∵A(-4,0),B(2,0),C(3,3),
∴DF=CE=3,OA=4,OE=3,OB=2,
∴OF=OA-AF=OA-BE=OA-(OE-OB)=4-(3-2)=3,
∴D(-3,3),
∵点D′与点D关于x轴对称,
∴D′(-3,-3),
把x=-3代入y=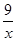 得,y=-3,
得,y=-3,
∴点D′在双曲线上;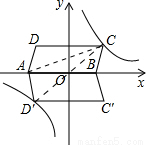
(3)∵C(3,3),D′(-3,-3),
∴点C和点D′关于原点O中心对称,
∴D′O=CO=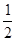 D′C,
D′C,
∴S△AD′C=2S△AOC=2×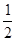 AO•CE=2×
AO•CE=2×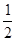 ×4×3=12,
×4×3=12,
即S△AD′C=12.


科目:初中数学 来源:2014中考名师推荐数学实数(解析版) 题型:解答题
(1)一个正数的平方根是a+3与2a﹣15,求a的值.
(2)已知 ,求
,求 的立方根.
的立方根.
(3)已知x、y为实数,且 .求
.求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的相似(解析版) 题型:选择题
如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )


A.(6,0) B.(6,3)
C.(6,5) D.(4,2)
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形与坐标(解析版) 题型:填空题
如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为 (用n表示).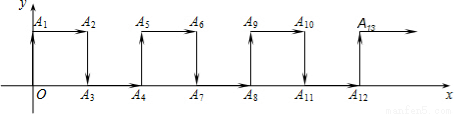
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学反比例函数(解析版) 题型:选择题
如图,点B在反比例函数y= 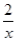 (x>0)的图象上,横坐标为1,过点B分别向x轴,y轴作垂线,垂足分别为A,C,则矩形OABC的面积为( )
(x>0)的图象上,横坐标为1,过点B分别向x轴,y轴作垂线,垂足分别为A,C,则矩形OABC的面积为( )

A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学分类讨论思想(解析版) 题型:选择题
某园艺公司对一块直角三角形的花园进行改造,测得两直角边长分别为a=6米,b=8米.现要将其扩建成等腰三角形,且扩充部分是以b为直角边的直角三角形,则扩建后的等腰三角形花圃的周长为( )米.
A.32或20+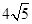
B.32或36或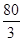
C.32或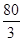 或20+
或20+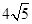
D.32或36或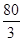 或20+
或20+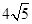
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学三角形(一)(解析版) 题型:填空题
如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是 .
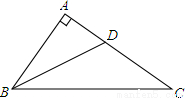
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com