
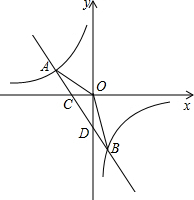
 一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C.已知点A(-2,1),点B的坐标为(1,m).
一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C.已知点A(-2,1),点B的坐标为(1,m).分析 (1)根据待定系数法,可得反比例函数解析式,再根据图象上的点满足函数解析式,可得B点坐标,再根据待定系数法,可得一次函数的解析式;
(2)根据三角形割补法,可得两个三角形,根据三角形面积的和差,可得答案;
(3)根据函数与不等式的关系:图象在下方的部分函数值小,可得答案.
解答 解:(1)将A点坐标代入反比例函数解析式,得
k=-2.
反比例函数解析式为y=-$\frac{2}{x}$,
将B点坐标代入反比例函数解析式,得m=-$\frac{2}{1}$,B(1,-2).
设AB的解析式为y=kx+b,将A、B点坐标代入函数解析式,得
$\left\{\begin{array}{l}{-2k+b=1}\\{k+b=-2}\end{array}\right.$.解得$\left\{\begin{array}{l}{k=-1}\\{b=-1}\end{array}\right.$,
一次函数的解析式为y=-x-1;
(2)直线AB与x轴的交点为C(-1,0),
S△AOB=S△AOC+S△BOC,即
$\frac{1}{2}$×|-1|×1+$\frac{1}{2}$×|-1|×|-2|=$\frac{3}{2}$;
(3)由一次函数图象在反比例函数图象下方部分,得
-2<x<0或x>1.
点评 本题考查了反比例函数与一次函数的交点,利用待定系数法求函数解析式,利用函数与不等式的关系求不等式的解集;利用分割法求三角形的面积是解题关键.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:解答题
 如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).
如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
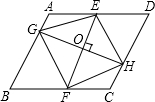 如图,点O是?ABCD的对称中心,过点O作两条互相垂直的直线EF,GH,分别与?ABCD的四条边交于点E,F和点G,H,试说明四边形EGFH是中心对称图形,它有几条对称轴.
如图,点O是?ABCD的对称中心,过点O作两条互相垂直的直线EF,GH,分别与?ABCD的四条边交于点E,F和点G,H,试说明四边形EGFH是中心对称图形,它有几条对称轴.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若$\frac{\sqrt{x-1}}{x-2}$有意义,则有x≥1且x≠2 | B. | 勾股定理是a2+b2=c2 | ||
| C. | 夹在两条平行线间的线段相等 | D. | a0=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
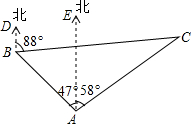 某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西47°方向,距A船26海里的海域,C船位于A船的北偏东58°方向,同时又位于B船的北偏东88°方向.
某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西47°方向,距A船26海里的海域,C船位于A船的北偏东58°方向,同时又位于B船的北偏东88°方向.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com