
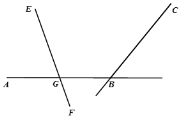
【题目】如图,直线AB与直线BC交于B点,∠ABC=n°(n>110),直线EF与直线AB交于点G,与直线BC交于H点,∠AGE=70°,将EF向右平移,在平移的过程中,∠GHC=_______°(用含n的式子表示)
【答案】n-70或250-n
【解析】
根据三角形外角的性质,分当H在直线AB下方时,当H在直线AB上方时两种情况解答即可.
解:在平移过程中,
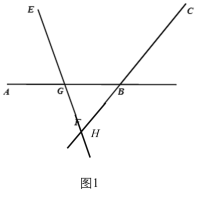
当H在直线AB下方时,如图,
∵∠ABC=∠GHC+∠HGB=∠GHC+∠AGE,∠AGE=70°,∠ABC=n°,
∴∠GHC=∠ABC-∠AGE=n°-70°;
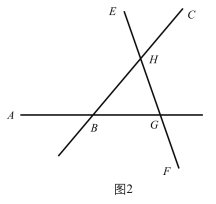
当H在直线AB上方时,如图,
∵∠ABC=∠AGE +∠BHG,
∠GHC=∠AGE+∠CBG,
∠AGE=70°,∠ABC=n°,
∴∠ABC+∠GHC=∠AGE +∠BHG+∠AGE+∠CBG=180°+∠AGE=180°+70°=250°,
∴∠GHC=∠ABC-∠AGE=250°-n°;
故答案为:n-70或250-n.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
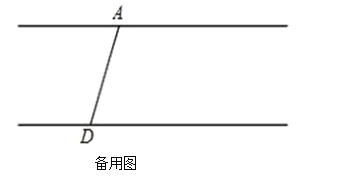
【题目】AB∥CD,C在 D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在的直线交于点 E.∠ADC=70°.
(1)求∠EDC 的度数;
(2)若∠ABC=30°,求∠BED 的度数;
(3)将线段 BC沿 DC方向移动,使得点 B在点 A的右侧,其他条件不变,若∠ABC=n°,请直接写出∠BED 的度数(用含 n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动到点A停止,设点P运动路程为x,△ABP的面积为y,如果y关于x的函数图象如图(2)所示,则矩形ABCD的面积是( )
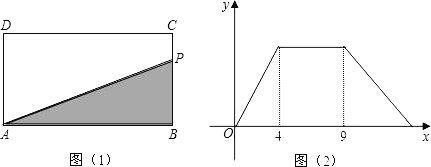
A. 10B. 16C. 20D. 36
查看答案和解析>>
科目:初中数学 来源: 题型:
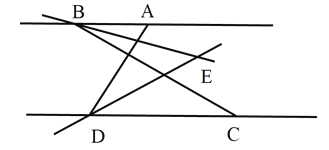
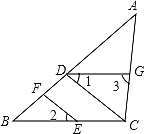
【题目】如图,点D、F在线段AB上,点E、G分别在线段BC和AC上,CD∥EF,∠1=∠2.
(1)判断DG与BC的位置关系,并说明理由;
(2)若DG是∠ADC的平分线,∠3=85°,且∠DCE:∠DCG=9:10,AB与CD有怎样的位置关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
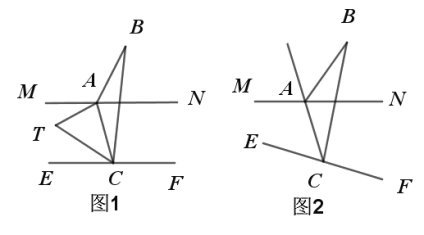
【题目】已知点A和点C分别在直线MN和直线EF上,点B在直线外,∠BAN=α,∠BCF=β.
(1)如图1,若MN∥EF,则∠B= (用α,β的式子表示,不写证明过程)
(2)在(1)的条件下,点T在直线MN与直线EF之间,∠MAT=![]() ∠BAN,∠TCB=2∠TCE,求∠B与∠T之间的数量关系.
∠BAN,∠TCB=2∠TCE,求∠B与∠T之间的数量关系.
(3)如图2,若MN不平行于EF,直线AC平分∠MAB,且平分∠ECB,则∠B= (用α,β的式子表示,不写证明过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校实行学案式教学,需印制若干份教学学案.印刷厂有,甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示.
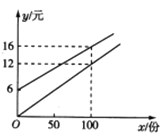
(1)填空:甲种收费方式的函数关系式是__________,乙种收费方式的函数关系式是__________.
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,边
中,边![]() 厘米,若动点
厘米,若动点![]() 从点
从点![]() 开始,按
开始,按![]() 的路径运动,且速度为1厘米/秒,设点
的路径运动,且速度为1厘米/秒,设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
(1)当![]() 时,判断
时,判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)当![]() 的面积为
的面积为![]() 面积的一半时,求
面积的一半时,求![]() 的值;
的值;
(3)另有一点![]() ,从点
,从点![]() 开始,按
开始,按![]() 的路径运动,且速度为
的路径运动,且速度为![]() 厘米/秒,若
厘米/秒,若![]() 、
、![]() 两点同时出发,当
两点同时出发,当![]() 、
、![]() 中有一点到达终点时,另一点也停止运动.当
中有一点到达终点时,另一点也停止运动.当![]() 为何值时,直线
为何值时,直线![]() 把
把![]() 的周长分成相等的两部分.
的周长分成相等的两部分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 请画出△ABC关于原点对称的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com