
【题目】如图,点D、F在线段AB上,点E、G分别在线段BC和AC上,CD∥EF,∠1=∠2.
(1)判断DG与BC的位置关系,并说明理由;
(2)若DG是∠ADC的平分线,∠3=85°,且∠DCE:∠DCG=9:10,AB与CD有怎样的位置关系?并说明理由.
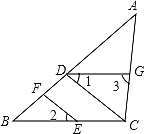
【答案】(1) DG∥BC.理由见解析. (2) CD⊥AB.理由见解析.
【解析】
(1)先根据CD∥EF得出∠2=∠BCD,再由∠1=∠2得出∠1=∠BCD,进而可得出结论;
(2)根据DG∥BC,∠3=85°得出∠BCG的度数,再由∠DCE:∠DCG=9:10得出∠DCE的度数,根据DG∥BC可得∠1=∠DCE,求出∠1的度数.由DG是∠ADC的平分线可得出∠ADC的度数,由此得出结论.
(1)DG∥BC.
理由:∵CD∥EF,
∴∠2=∠BCD.
∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC;
(2)CD⊥AB.
理由:∵由(1)知DG∥BC,∠3=85°,
∴∠BCG=180°-85°=95°.
∵∠DCE:∠DCG=9:10,
∴∠DCE=95°×![]() =45°
=45°
∴∠1=∠DCE=45°
∵DG是∠ADC的平分线,
∴∠ADC=2∠1=90°,
∴CD⊥AB.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在△ABC和△DEF中,将△DEF按要求摆放,使得∠D的两条边分别经过点B和点C.
(1)当将△DEF如图1摆放时,若∠A=50°,∠E+∠F=100°,则∠D= ;∠ABD+∠ACD= .
(2)当将△DEF如图2摆放时,∠A=m°,∠E+∠F=n°,请求出∠ABD+∠ACD的度数(用含m、n的代数式表示).
(3)能否将△DEF摆放到某个位置,使得BD、CD同时平分∠ABC和∠ACB.若能,求出∠A、∠E、∠F满足的关系?若不能,请说明理由?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆拥有客房90间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元) | 200 | 240 | 270 | 300 |
y(间) | 90 | 70 | 55 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房,宾馆每日需支出60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入﹣当日支出)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读第(1)题解答过程填理由,并解答第(2)题
(1)已知:如图1,AB∥CD,P为AB,CD之间一点,求∠B+∠C+∠BPC的大小.
解:过点P作PM∥AB
∵AB∥CD(已知)
∴PM∥CD ,
∴∠B+∠1=180°, .
∴∠C+∠2=180°
∵∠BPC=∠1+∠2
∴∠B+∠C+∠BPC=360°
(2)我们生活中经常接触小刀,如图2小刀刀柄外形是一个直角梯形挖去一个小半圈,其中AF∥EG,∠AEG=90°,刀片上、下是平行的(AB∥CD),转动刀片时会形成∠1和∠2,那么∠1+∠2的大小是否会随刀片的转动面改变,如不改变,求出其大小;如改变,请说明理由.
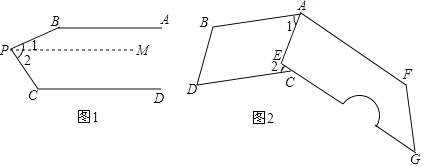
查看答案和解析>>
科目:初中数学 来源: 题型:
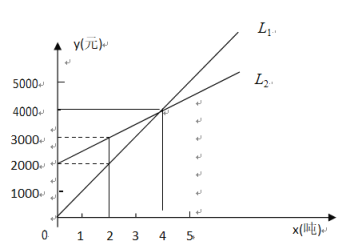
【题目】如图,图象![]() 反映了某公司产品的销售收入与销售量之间的关系,图象
反映了某公司产品的销售收入与销售量之间的关系,图象![]() 反映了某公司产品的销售成本与销售量之间的关系,则:
反映了某公司产品的销售成本与销售量之间的关系,则:
(1)当销售量为2吨时,销售收入为多少元?销售成本呢?此时公司是赢利还是亏损?
(2)当销售量等于多少时该公司收入等于销售成本?
(3)当销售量在什么范围内时,该公司亏损?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b和反比例函数y= ![]() 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
A.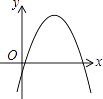
B.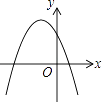
C.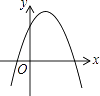
D.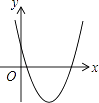
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与直线BC交于B点,∠ABC=n°(n>110),直线EF与直线AB交于点G,与直线BC交于H点,∠AGE=70°,将EF向右平移,在平移的过程中,∠GHC=_______°(用含n的式子表示)
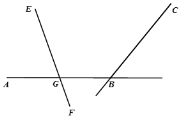
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,在![]() 中,
中,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,有下列说法:①点
,有下列说法:①点![]() 与点
与点![]() 的距离是线段
的距离是线段![]() 的长;②点
的长;②点![]() 到直线
到直线![]() 的距离是线段
的距离是线段![]() 的长;③线段
的长;③线段![]() 是
是![]() 边
边![]() 上的高;④线段
上的高;④线段![]() 是
是![]() 边
边![]() 上的高.
上的高.
上述说法中,正确的个数为( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①倒数等于本身的数是±1;②互为相反数的两个非零数的商为﹣1;③如果两个数的绝对值相等,那么这两个数相等;④有理数可以分为正有理数和负有理数;⑤单项式﹣![]() 的系数是﹣
的系数是﹣![]() ,次数是6;⑥多项式3πa3+4a2﹣8是三次三项式,其中正确的个数是( )
,次数是6;⑥多项式3πa3+4a2﹣8是三次三项式,其中正确的个数是( )
A. 2 个B. 3 个C. 4 个D. 5 个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com