
【题目】已知OP平分∠AOB,点Q在OP上,点M在OA上,且点Q,M均不与点O重合.在OB上确定点N,使QN =QM,则满足条件的点N的个数为( )
A.1 个B.2个C.1或2个D.无数个
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
为响应市政府“绿色出行”的号召,小张上班由自驾车改为骑公共自行车.已知小张家距上班地点10千米.他用骑公共自行车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程少45千米,他从家出发到上班地点,骑公共自行车方式所用的时间是自驾车方式所用的时间的4倍.小张用骑公共自行车方式上班平均每小时行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C,AB=16cm,BC=12cm,D为AB的中点.若点P在线段BC上以4cm/s的速度由B向C运动,同时,点Q在线段CA上以a(cm/s)的速度由C向A运动,设运动的时间为t(s)(0≤t≤3)

(1)用关于t的代数式表示PC的长度.
(2)若点P,Q的运动速度相等,经过1s后,△BPD与△CQP是否全等?请说明理由.
(3)若点PQ的运动速度不相等,当点Q的运动速度a为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x+3)(x﹣1)(a≠0),与x轴从左至右依次相交于A、B两点,与y轴相交于点C,经过点A的直线y=﹣![]() x+b与抛物线的另一个交点为D.
x+b与抛物线的另一个交点为D.
(1)若点D的横坐标为2,求抛物线的函数解析式;
(2)若在第三象限内的抛物线上有点P,使得以A、B、P为顶点的三角形与△ABC相似,求点P的坐标;
(3)在(1)的条件下,设点E是线段AD上的一点(不含端点),连接BE.一动点Q从点B出发,沿线段BE以每秒1个单位的速度运动到点E,再沿线段ED以每秒![]() 个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?
个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形纸片ABC中,∠B=90°,∠A=30°,AC=4,点E在AC上,AE=3.将三角形纸片按图1方式折叠,使点A的对应点![]() 落在AB的延长线上,折痕为ED,
落在AB的延长线上,折痕为ED,![]() 交BC于点F.
交BC于点F.
(1)求∠CFE的度数;
(2)如图2,,继续将纸片沿BF折叠,点![]() 的对应点为
的对应点为![]() ,
,![]() 交DE于点G .求线段DG的长.
交DE于点G .求线段DG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,点D,E分别在AB,AC上,补充下列一个条件后,不能判断△ABE ≌△ACD的是

A.∠B=∠CB.AD=AEC.∠BDC=∠CEBD.BE=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某建筑公司甲、乙两个工程队共同参与一项改造工程.已知甲队单独完成这项工程的时间是乙队单独完成这项工程时间的1.5倍,由于乙队还有其他任务,先由甲队单独做45天后,再由甲、乙两队合做30天,完成了该项改造工程任务.
(1)求甲、乙两队单独完成改造工程任务各需多少天;
(2)这项改造工程共投资240万元,如果按完成的工程量付款,那么甲、乙两队可获工程款各多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
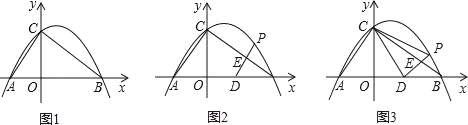
【题目】已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上(如图1).
(1)求线段OA、OB的长和经过点A、B、C的抛物线的关系式.
(2)如图2,点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点(其中m>0,n>0),连接DP交BC于点E.
①当△BDE是等腰三角形时,直接写出此时点E的坐标.
②又连接CD、CP(如图3),△CDP是否有最大面积?若有,求出△CDP的最大面积和此时点P的坐标;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com