
����Ŀ��ij������˾�ס����������̶ӹ�ͬ����һ����칤��.��֪�ӵ����������̵�ʱ�����Ҷӵ�����������ʱ���1.5���������Ҷӻ��������������ɼӵ�����45������ɼס������Ӻ���30�죬����˸�����칤������.
��1����ס������ӵ�����ɸ��칤�������������죻
��2��������칤�̹�Ͷ��240��Ԫ���������ɵĹ����������ô�ס������ӿɻ̿��������Ԫ��
���𰸡���1���ס������ӵ�����ɸ��칤���������120�졢80�죻��2���ӻ�ù��̿�Ϊ150��Ԫ���Ҷӻ�ù��̿�Ϊ90��Ԫ.
��������
��1�����Ҷӵ�����������ʱ��Ϊ![]() �죬�ɵüӵ�����������ʱ��Ϊ1.5x�죬�������ɼӵ�����45������ɼס������Ӻ���30�죬����˸�����칤�������з�ʽ�������x��ֵ���������1.5x��ֵ���ɵô𰸣�
�죬�ɵüӵ�����������ʱ��Ϊ1.5x�죬�������ɼӵ�����45������ɼס������Ӻ���30�죬����˸�����칤�������з�ʽ�������x��ֵ���������1.5x��ֵ���ɵô𰸣�
��2���������ӵĹ���Ч�ʿɵ����ӵĹ�����ռ���������ı���������240���ɵô�.
��1�����Ҷӵ�����������ʱ��Ϊ![]() ��.
��.
�ӵ����������̵�ʱ�����Ҷӵ�����������ʱ���1.5����
��ӵ�����������ʱ��Ϊ1.5x�죬
�����ɼӵ�����45������ɼס������Ӻ���30�죬����˸�����칤������
��![]()
��ã�![]()
�����飬![]() ��ԭ���̵Ľ�.
��ԭ���̵Ľ�.
![]()
�𣺼ס������ӵ�����ɸ��칤���������120�졢80��.
��2���ӻ�ù��̿�Ϊ��![]() ��Ԫ��
��Ԫ��
�Ҷӻ�ù��̿�Ϊ��![]() ��Ԫ.
��Ԫ.


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪Rt��AOB������ֱ�DZ�0A��08�ֱ���y���x���ϣ�����OA��OB�ij��ֱ��Ƿ���x2��7x+12=0������(OA<0B)������P�ӵ�A��ʼ���߶�AO����ÿ��l����λ���ȵ��ٶ����O�˶���ͬʱ������Q�ӵ�B��ʼ���߶�BA����ÿ��2����λ���ȵ��ٶ����A�˶������P��Q�˶���ʱ��Ϊt�룮
(1)��A��B��������ꡣ
(2)��tΪ��ֵʱ����APQ����AOB���ƣ���ֱ��д����ʱ��Q�����꣮
(3)��t=2ʱ��������ƽ���ڣ��Ƿ���ڵ�M��ʹ��A��P��Q��MΪ������ı�����ƽ���ı���?�����ڣ���ֱ��д��M������ꣻ�������ڣ���˵�����ɣ�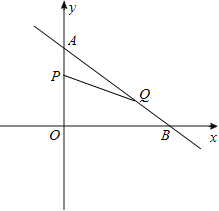
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪OPƽ�֡�AOB����Q��OP�ϣ���M��OA�ϣ��ҵ�Q,M�������O�غ�.��OB��ȷ����N��ʹQN =QM�������������ĵ�N�ĸ���Ϊ�� ��
A.1 ��B.2��C.1��2��D.������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һԪ���η���x2+��1��2m��x+m+13=0������֮����������֮�͵�2������m��ֵ�ǣ�������
A. ��5 B. 5 C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���չ�˾��ӪA��B��C��D�ĸ�����֮��Ŀ���ҵ������Ʊ�۸�y��Ԫ���������м�ľ���x��ǧ�ף���һ�κ�������������һ���ڼ䲿�ֻ�Ʊ�۸����±���ʾ��
��� | �յ� | ����x��ǧ�ף� | �۸�y��Ԫ�� |
A | B | 1000 | 2050 |
A | C | 800 | 1650 |
A | D | 2550 | |
B | C | 600 | |
C | D | 950 |
��1����ù�˾��Ʊ�۸�y��Ԫ�������x��ǧ�ף��ĺ�����ϵʽ��
��2�����ã�1���еĹ�ϵʽ��������������
��3���ж�A��B��C��D���ĸ������У�������������ͬһ��ֱ���ϣ���˵�����ɣ�
��4�������չ�˾��������������7�¿�ʼ������B��ֱ�ӷɵ�D�е�����ר�ߣ��Ұ����Ϲ��ɸ���Ʊ���ۣ���ô��Ʊ����Ӧ�Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�����ABCD���Խ���AC��Ϊ����ֱ�������Σ�AB=3��BC=6���ֽ�Rt��ADC�Ƶ�C˳ʱ����ת90������A��ת���λ��Ϊ��E����D��ת���λ��Ϊ��F����CΪԭ�㣬��BC����ֱ��Ϊx�ᣬ�Թ���C��ֱ��BC��ֱ��Ϊy�ᣬ������ͼ�ڵ�ƽ��ֱ������ϵ��

��1����ֱ��AE�Ľ���ʽ��
��2����Rt��EFC��x��ĸ�����ƽ���ƶ�����ͼ�ۣ���OC=x��0��x��9����Rt��EFC��Rt��ABO���ص��������Ϊs����x=1��x=8ʱ��s��ֵ��
��3���ڣ�2����������s�Ƿ�������ֵ�������ڣ����������ֵ����ʱx��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
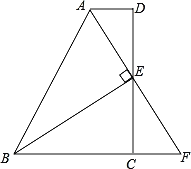
����Ŀ����ͼ�����ı���ABCD�У�AD��BC��EΪCD���е㣬����AE��BE��BE��AE���ӳ�AE��BC���ӳ����ڵ�F��
��֤��(1)FC��AD��(2)AB��BC+AD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����С��һ��Բ���ε���ˮ�ܵ����ѣ�ά����ԱΪ�����ܵ�����ȷ���ܵ�Բ�ν���İ뾶����ͼ��ˮƽ���õ����ѹܵ���ˮ���ֵĽ��森
�����㲹ȫ�����ˮ�ܵ���Բ�ν��棻
���������ˮ�ܵ���ˮ���ֵ�ˮ���AB��16cm��ˮ������ط��ĸ߶�Ϊ4cm�������Բ�ν���İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��l��y=x+![]() ��x�Ḻ���ᡢy��������ֱ��ཻ��A��C���㣬������y=��
��x�Ḻ���ᡢy��������ֱ��ཻ��A��C���㣬������y=��![]() x2+bx+c������B��1��0���͵�C��
x2+bx+c������B��1��0���͵�C��

��1���������ߵĽ���ʽ��
��2����֪��Q��������y=��![]() x2+bx+c�ڵڶ������ڵ�һ�����㣮
x2+bx+c�ڵڶ������ڵ�һ�����㣮
����ͼ1������AQ��CQ�����Q�ĺ�����Ϊt����AQC�����ΪS����S��t�ĺ�����ϵʽ�������S�����ֵ��
������BQ��AC�ڵ�D������BC����BDΪֱ������I���ֱ�BC��AB�ڵ�E��F������EF�����߶�EF����Сֵ����ֱ��д����ʱ��Q�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com